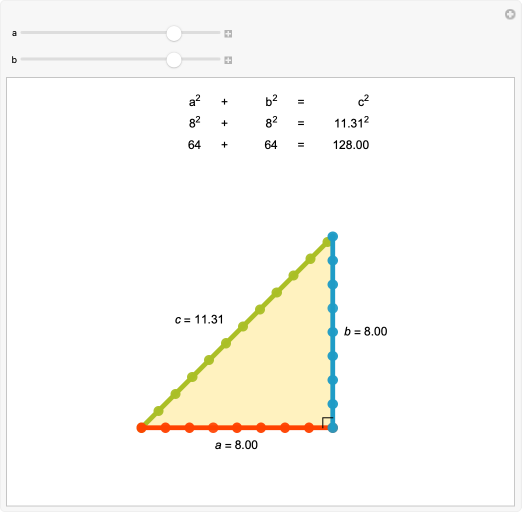
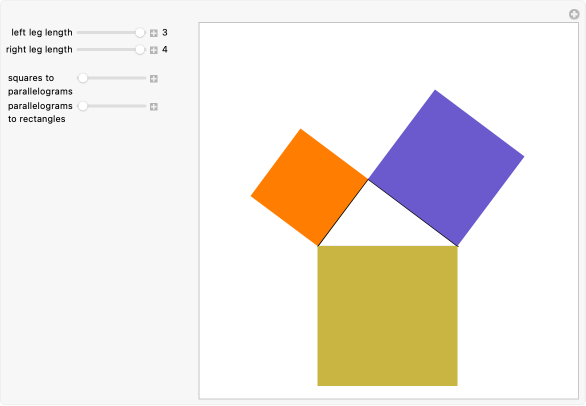
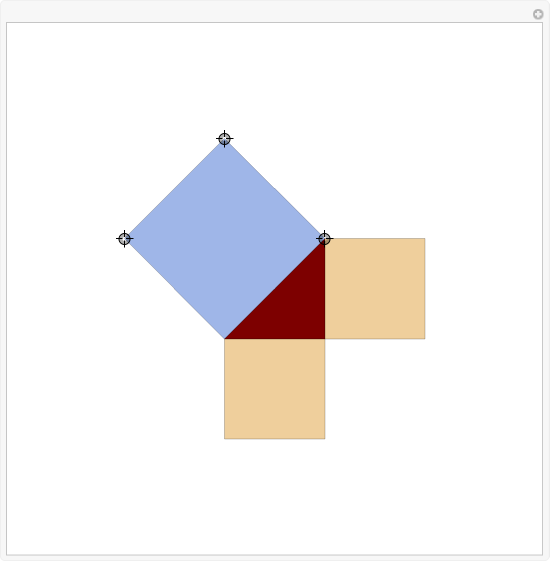
The Pythagorean theorem is one of the oldest and most important results in mathematics. The theorem states that if a triangle has one right angle, then the square of the longest side, called the hypotenuse, is equal to the sum of the squares of the lengths of the two shorter sides, called the legs. So if a and b are the lengths of the legs, and c is the length of the hypotenuse, then a² + b² = c². The following is a simple geometrical proof by rotation; the area of the squares a² and b² is equivalent to the resulting square c².

This relationship was known to the ancient scholars and builders of Babylonia, Egypt, China and India. While Pythagoras lived from 569–475 BCE, the result that now bears his name appeared as early as 1800 BCE in clay Babylonian tablets. The Pythagorean theorem was also known to early Chinese scholars and appeared in the sacred texts of ancient India related to altar building. This remarkable property of right triangles a² + b² = c² was probably discovered by looking at the simplest case, the 3–4–5 right triangle:

Knowing that the right triangle obtained from three sticks of 3, 4 and 5 units of length has square sides measuring 3² = 9, 4² = 16 and 5² = 25, they were probably led to consider whether a similar relation to 3² + 4² = 5² was true of the sides of other right triangles. The simplest case to investigate was that of a right triangle with equal legs, a = b. In this case, the proof would easily appear from a square split into eight right triangles, as depicted in problems 10 and 11 in the Babylonian geometrical problem tablet:

Right angles are part of the most primitive experience of the world: gravity is vertical, and the horizon stands at right angles to it. No one knows how or when the Pythagorean theorem was first discovered, but it happened long before Pythagoras. Archaeologists have found the theorem on tablets in Mesopotamia dating from the first half of the second millennium BCE, a thousand years before his lifetime. It was already so well known then that it was being taught in scribal schools.

Egyptian builders knew how to create square corners with an astounding degree of precision, perhaps by using a technique that earned them the nickname rope stretchers among their Greek contemporaries. There is a hint about what that meant in this wall painting from the Tomb of Menna.

Rope stretchers used 3–4–5 triangles and the plummet, which are still in use by modern surveyors. Rope-stretching technology spread to ancient Greece, India and China, where it stimulated the development of geometry. Recall that geometry comes from two Greek words: geo means "Earth" and -metria means "to measure." So geometry was originally the art of earth measuring, what we nowadays would call topography.

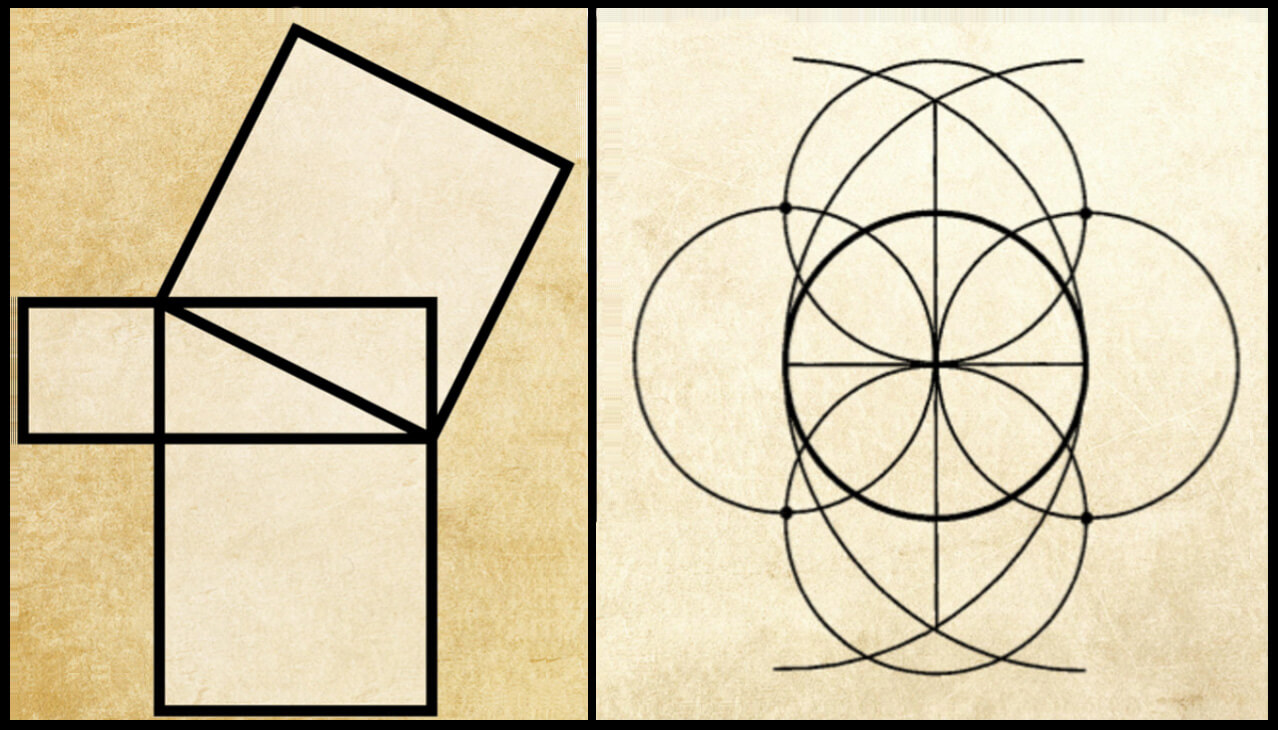
In India, right triangles appeared in the designs on Vedic sacrificial altars dating from as early as 1000 BCE. A collection of Vedic texts called the Śulbasūtras  (rules of the rope), dating from between 500 and 200 BCE, told how to construct these altars and how to enlarge them while retaining the same proportions. Enlarging the altar was a way of seeking protection from the god or gods, and getting the right response depended on keeping the exact proportions. The Pythagorean theorem does not appear in the manuals, but the writers seem to have been aware of it.

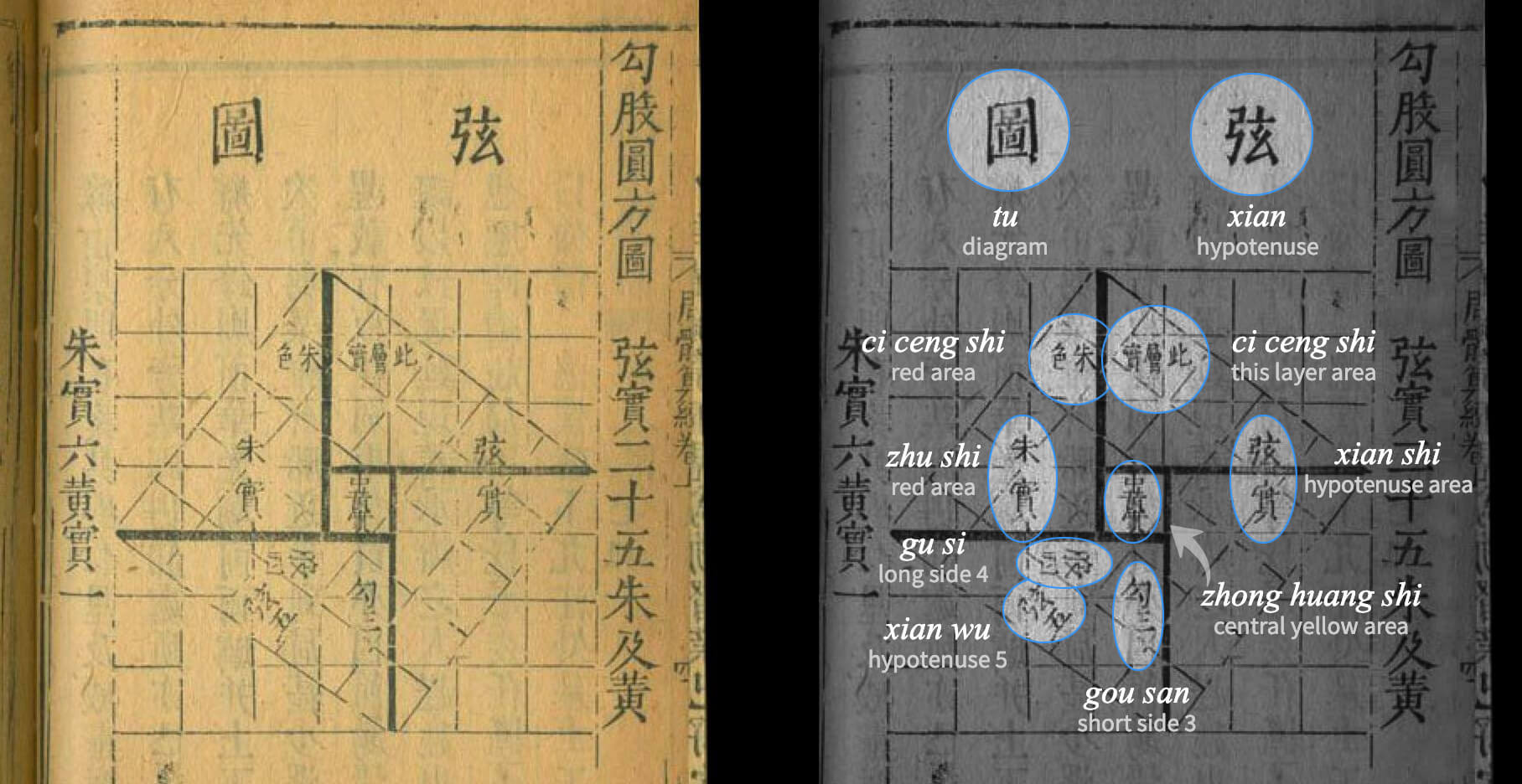
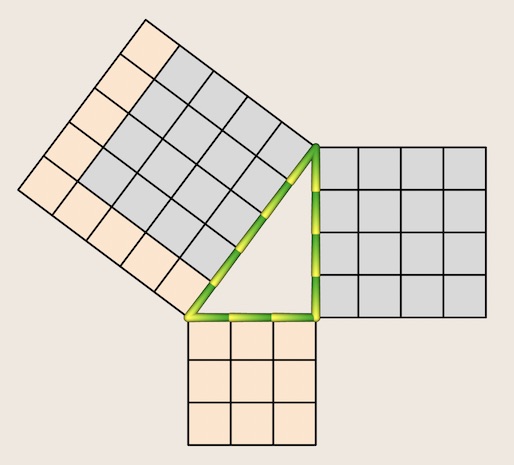
In China, the Pythagorean theorem has been known for millennia as the Gou-Gu rule. The earliest extant Chinese text on astronomy and mathematics, Zhoubi Suanjing, is notable for a diagrammatic demonstration of the theorem. The figure used to prove the theorem in Zhoubi Suanjing is usually referred to as the hypotenuse diagram, or xian tu. It is ascribed to Zhen Luan (535–566), a Chinese mathematician and astronomer who mentions the diagram while discussing Zhao Shuang's third-century commentary of Zhoubi Suanjing. The following is a dissection proof of the Gou-Gu rule, often described as the process of piling up the rectangles.

Another important mathematical text from ancient China is The Nine Chapters on the Mathematical Art, a book composed by several generations of scholars from the 10th–2nd century BCE. Entries in the book usually take the form of a statement of a problem, followed by the statement of the solution and an explanation of the procedure that led to the solution. For example, problem 13, the broken bamboo problem, considers an upright bamboo stalk 10 chi high that is fixed at the base and broken partway up its height. While the rooted portion below the break is left in place, the upper fragment of the stalk is bent over at the break point until it touches the ground 3 chi to the right of the base. The solution to the problem involves the application of the Gou-Gu rule.

The bamboo problem also appears in the ninth-century Sanskrit mathematical classic The Ganita-sara-samgraha by Mahavira. It reappears again in the first printed book to accompany mathematical problems with illustrations, Filippo Calandri's 1491 Aritmetica.

Similar geometrical problems are found in Bhāskara II's treatise on mathematics, written in 1150.

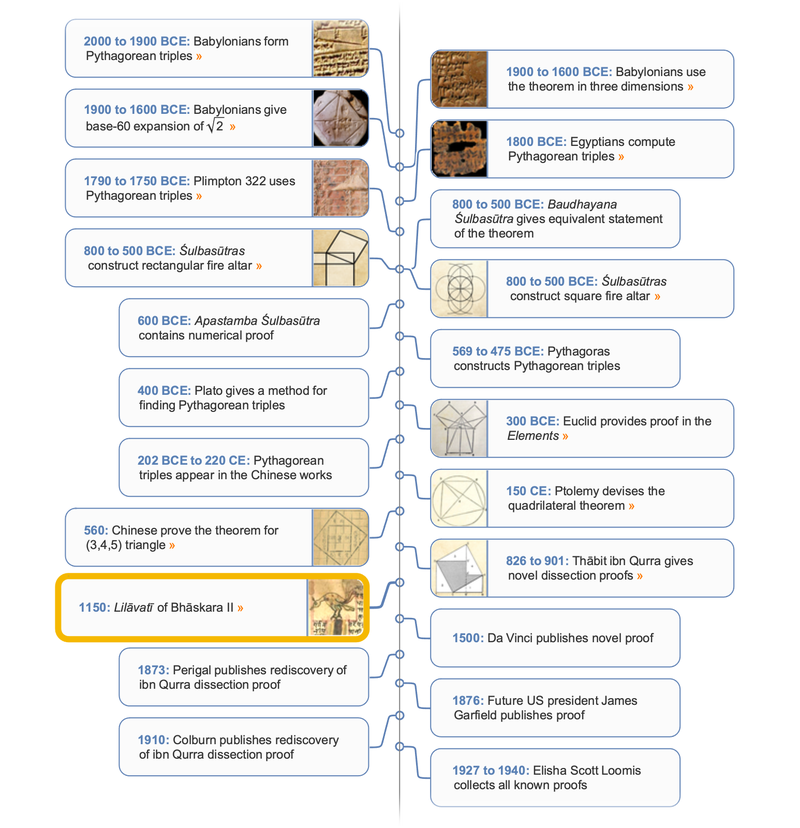
In the West, the most widespread proof of the Pythagorean theorem is found in Book I, Propositions 47 of Euclid's Elements, written around 300 BCE. This is a remarkably clever proof involving the contents of Book I only. Novel proofs of the theorem, including ibn Qurra's proofs, have been discovered from time to time ever since. With hundreds of different proofs, the Pythagorean theorem has more published proofs than any other theorem!