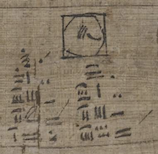
around1900–1000 BCE
Funding for this project generously provided by Overdeck Family Foundation
One of the most fascinating discoveries in geometry happens when we notice that circles can be used to make lots of different shapes.
In this photo, captured by photographer David Marvin, we can see that a stick got swept around by the wind and made a circle in the sand. We can use this to look at a cool example of making shapes with circles. If we add six other sticks of the same length as the stick that made the radius of the circle around the edges of the circle, we can make a hexagon!
If we know that we can make a hexagon inside of every circle when its sides are the same length as the radius, then we can make a fair approximation of the numerical value of π.
Let's say that the sticks that make up the radius r of the circle and the sides of the hexagon are all half a unit long.
That means that the hexagon's perimeter is made up of six half-units: ![]() .
.
We know that the circumference of a circle is found using the formula 2π r, so if we substitute in the radius, then we get: ![]() .
.
From the image, we can tell that the hexagon's perimeter is slightly shorter than the circle's circumference, because the hexagon fits inside the circle.
So we know that π must be a little bit bigger than 3.
This fits with what we know! π is 3.14… a little bit bigger than 3!
Geometric Shapes in Ancient Mesopotamia
Geometric shapes were important in ancient Mesopotamia. Much of their art, sculpture and visual culture incorporated geometry and mathematical patterns. Let's have a look at some important shapes!
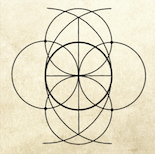
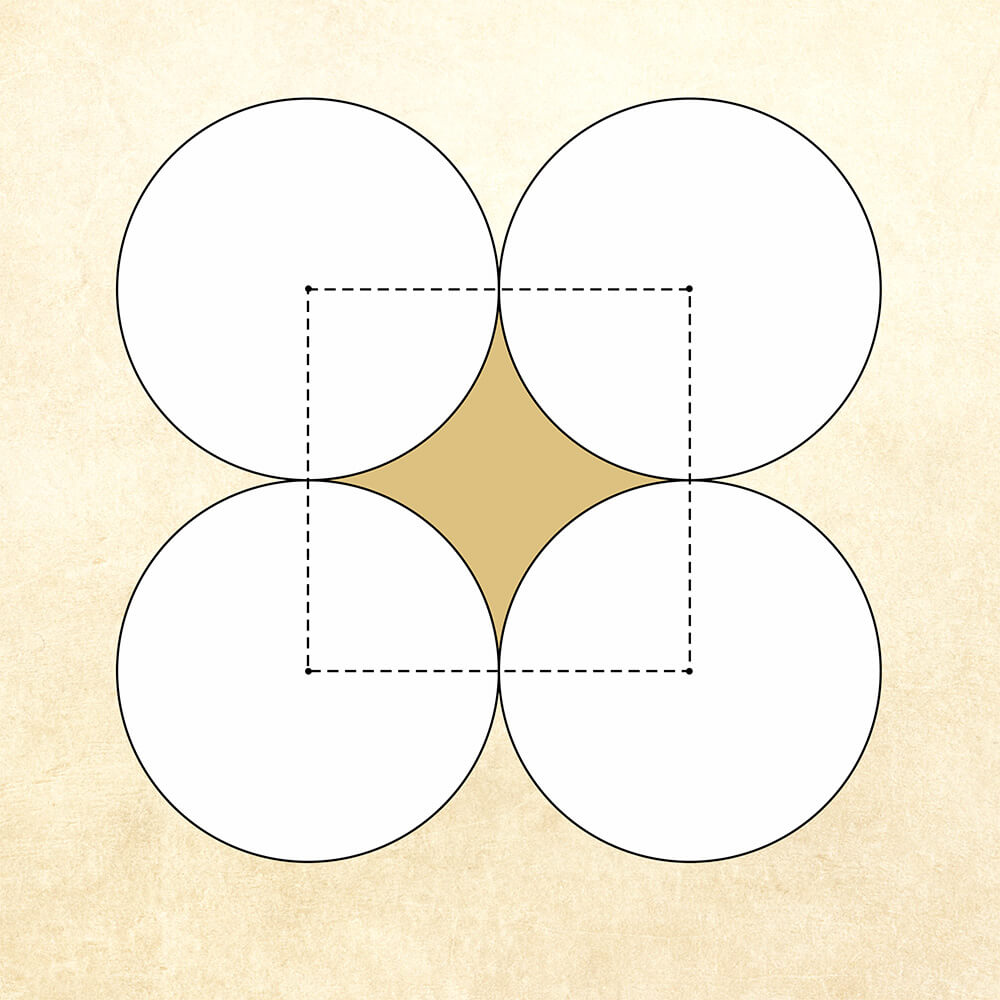
The apsamikku is the interior region of four identical circles, which you can see in gold here:
A number of basic geometric shapes like the hexagon and the apsamikku were everywhere in Mesopotamian and Babylonian visual cultures.
In addition to the hexagons and the flower shapes, you can see the apsamikku here in the bands with half-circles on the arms of the robe:

Like the hexagon, the apsamikku can be obtained from a circle. It emerges when we split a circle in four pieces and rearrange those into a square.

This shape might not seem too familiar to you in the modern world. In the 21st century, we are very comfortable with shapes like squares, circles and triangles. In ancient Mesopotamia, they had different shapes that were more familiar to them, including the apsamikku. We have actually inherited a lot of things from Mesopotamian mathematicians and scholars. In fact, things as basic as the seven-day week can be traced back to this culture. The ancient week was divided among the seven most powerful Mesopotamian deities: An, Enlil, Enki, Ninhursag, Nanna, Utu and Inanna.

Look at these images represented in geometric form.
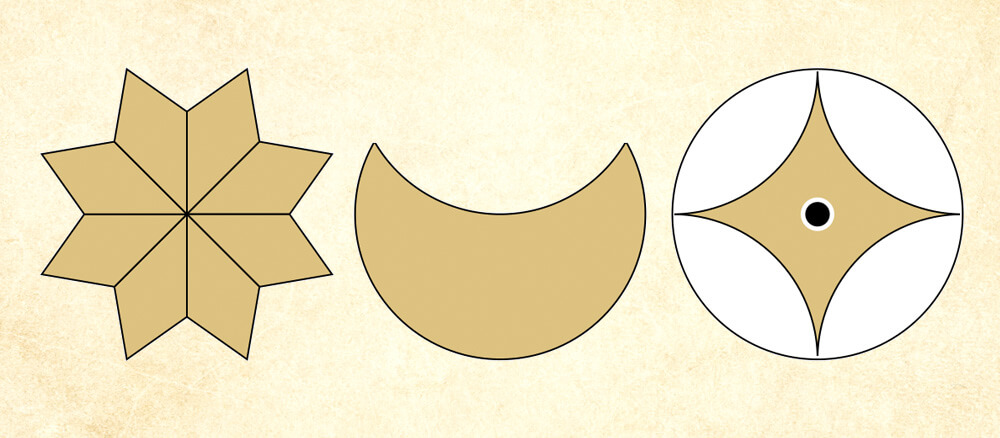
The first symbol is an eight-pointed star, which is the common symbolic representation for the goddess Inanna, the Queen of Heaven. She was associated with lions, the planet Venus, fertility and abundance.

The second symbol is the crescent moon, which represents Nanna, the Moon god.

The apsamikku was used to symbolize Utu, the Sun god. Utu was associated with qualities such as truth and justice, and Mesopotamian scholars associated geometry with these qualities too.
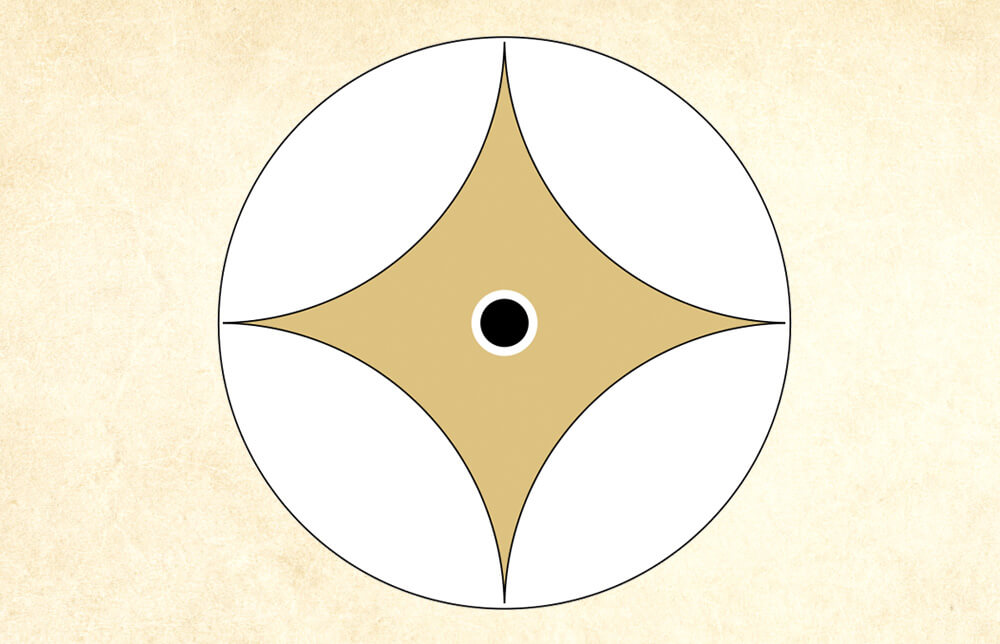
Look at the structure of the apsamikku and other geometric shapes. Learn more about these shapes on the Susa Mathematical Tablet TMS 3 exhibit page.
This interactive illustration shows the geometric structure of some shapes that were common in Mesopotamia: the apsamikku, the eight-pointed star, the crescent, the barley grain and the ox-eye.
A clay tablet with geometrical problems accompanied by diagrams, tablet BM 15285, has been instrumental in our understanding of Babylonian geometry. See the apsamikku on the bottom row.

This four-thousand-year-old tablet shows lots of interesting geometric figures that the ancient cultures were working out. In most cases, we can find each figure by rearranging the pieces of simple shapes like circles, squares and triangles. For example, problem 32 on the bottom-right of the tablet, gets reduced from the bulb-like shape into an apsamikku and a barley grain. Use the slider to move the pieces on the interactive shape below!
Squaring the Circle
A big problem in ancient geometry was figuring out how to show if a square can have an equal area to a shape with curved sides. The first mathematician on record to show a possible way to solve this problem was Hippocrates of Chios, a Greek merchant who lost all his property when he was captured by pirates.
Use the slider to show how these four crescent shapes have the same area as a square.
While Hippocrates's solution shows us that parts of a circle can have the same area as a square, it gave false hope for a long time that we could come up with a way to show that a circle can have the same area as a square. Squaring the circle was one of the most famous mathematical problems of antiquity, and has been of interest throughout the whole history of mathematics.
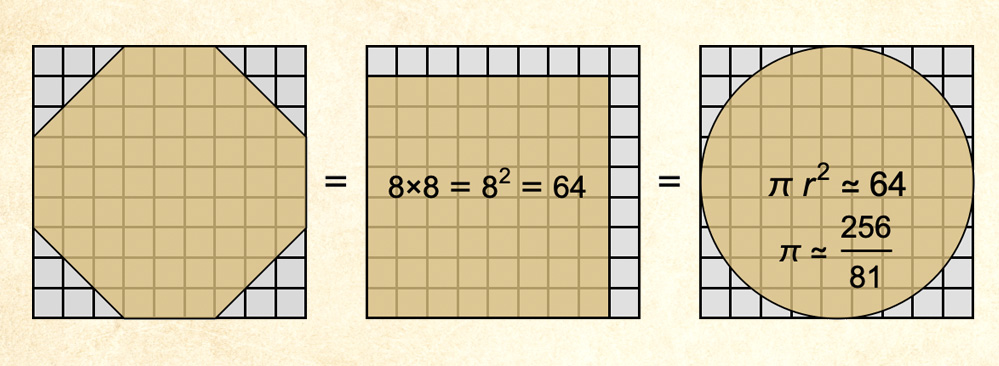
One of the oldest surviving mathematical writings is the Rhind papyrus. It is a scroll about six meters long and was written in Egypt about four thousand years ago. Part of the papyrus talks about a method to approximate the area of a circle with a square:

The solution in the Rhind papyrus is particularly notable because it computes the area of a circle by trying to solve for π using some approximations.
They find that the area of a square measuring 8 tiles by 8 tiles is 82, or 64.
They then estimate that the area of a circle with ![]() is the same as the area of the square with sides 8.
is the same as the area of the square with sides 8.
We know that the numerical value of π is approximately 3.14159…, so if we get the correct value of π when we say that the circle has the same area as the square, then we know that we have been able to square the circle.
Using the formula πr2 to find the area of the circle, they substitute r for ![]() .
.
If we work this out, we find:
![]()
In order to approximate π in this problem, we say that:
![]() = 64
= 64
When we calculate this out, we get that π = 256/81, which is 3.16049….
Disappointingly, 3.16049… isn't the same as 3.14159…, so the Rhind papyrus didn't manage to prove that the circle has the same area as the square.
It's only in modern times, more than two thousand years after the problem was formulated, that it was proved to be impossible!
However, if we include an apsamikku figure in the middle of the square, then we can at least pretend that we solved the problem!
Use the slider to move the pieces of the circle to form a square with an apsamikku in the center.
Find Out More About:
Visit the online History of Mathematics exhibit to learn more!
Further Reading
- Albenda, P. "55) On Geometry and Assyrian Decorative Designs." Nouvelles Assyriologiques Brèves et Utilitaires, No. 2 (June), pp. 101–103, 2017.
- Beckmann, P. A History of Pi. New York: Barnes & Noble, 1993.
- Lawergren, B. and Gurney, O. "Sound Holes and Geometrical Figures: Clues to the Terminology of Ancient Mesopotamian Harps." Iraq, Vol. 49, pp. 37–52, 1987.
- Friberg, J. A Remarkable Collection of Babylonian Mathematical Texts: Manuscripts in the Schøyen Collection: Cuneiform Texts I. New York: Springer, pp. 217–218, 2007.
- Friberg, J. and Al-Rawi, F. N. H. New Mathematical Cuneiform Texts. Springer, pp. 256–257, 325 and 396, 2016.
- Friberg, J. Amazing Traces of a Babylonian Origin in Greek Mathematics. Singapore: World Scientific, 2007.
- Gadd, C. J. "Forms and Colours." Revue d'Assyriologie et d'archéologie orientale, Vol. 19, pp. 149–159, 1922.
- Harper, P. O.; Aruz, J.; and Tallon, F. (eds.). The Royal City of Susa: Ancient Near Eastern Treasures in the Louvre. New York: The Metropolitan Museum of Art, pp. 276–278, 1992.
- Kordemsky, B. A. The Moscow Puzzles. London: Penguin, p. 238, 1990.
- Richeson, D. S. Tales of Impossibility: The 2000-Year Quest to Solve the Mathematical Problems of Antiquity. Princeton, NJ: Princeton University Press, 2019.
- Robson, E. "Appendix 2: BM 15285." In Mesopotamian Mathematics, 2100–1600 BC: Technical Constants in Bureaucracy and Education. Oxford, England: Clarendon Press, pp. 208–217, 1999.
- Robson, E. "Mesopotamian Mathematics: Mathematical Problems." Ch. 2, § III.b in The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook (Ed. V. Katz). Princeton, NJ: Princeton University Press, pp. 92–100, 2007.
- Robson, E. Mesopotamian Mathematics, 2100–1600 BC: Technical Constants in Bureaucracy and Education. Oxford, England: Clarendon Press, pp. 19–21, 48–50 and 199–201, 1999.
- Robson, E. "The Long Career of a Favorite Figure: The Apsamikku in Neo-Babylonian Mathematics." Ch. 14 in From the Banks of the Euphrates: Studies in Honor of Alice Louise Slotsky (Ed. M. Ross). University Park, PA: Eisenbrauns, pp. 211–226, 2008.
- Yuste, P. "Ancient Geometry: Thinking about How to Measure the Circle." Almagest, Vol. 2, No. 2, pp. 4–5, 2011.