From kites and hot-air balloons to massive modern planes, people have been trying to make machines that fly for over two thousand years. In the 1890s, Alexander Graham Bell, the inventor of the telephone, began experimenting with giant kites that were big enough to lift a person and a motor into the air. Bell's kites were made up of lots of repeating shapes.

One of the major problems Bell had with trying to make a flying machine was a mathematical one. He had to try to make a shape that had proportionally the same area, weight and volume even as they scaled up. In other words, he needed to make a shape that, no matter how big you made it, was always going to have the correct surface-area-to-weight ratio to make flight possible.

To find out how Bell chose the weird and wonderful shape he chose for his flying machine, we need to go back in time to the ancient Greeks, where philosophers and mathematicians were working on the square-cube problem.

Socrates Teaches Geometry

Socrates, an ancient Greek philosopher, had a theory that learning, especially when you're learning fundamental truths about the universe—like math—was actually just remembering knowledge that was always in your brain. He tried to prove this by asking a young boy with no math knowledge to solve a geometry problem for him.

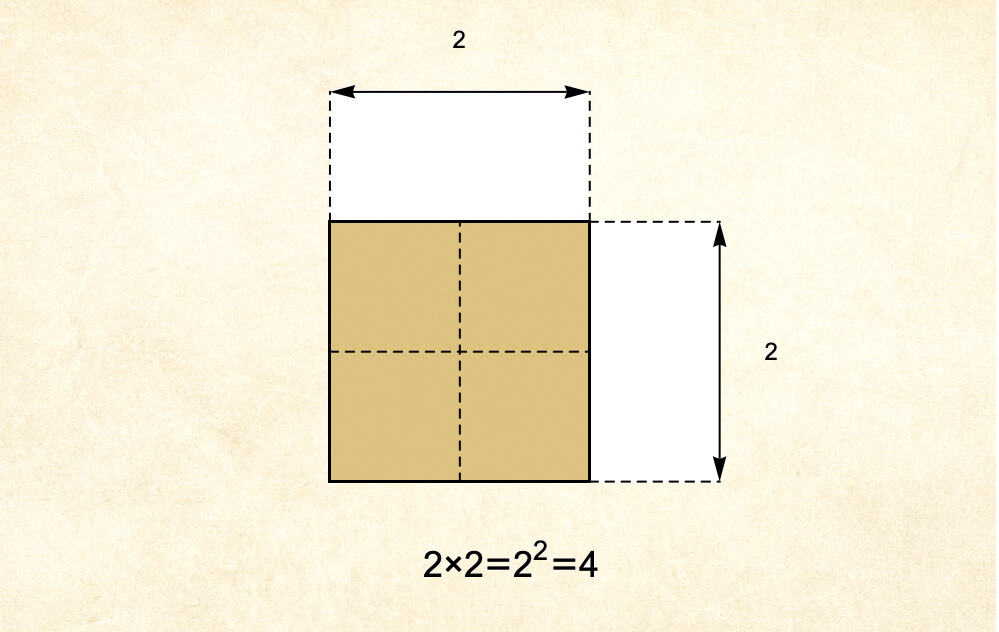
Socrates drew a square on the ground and showed the boy the four sides before dividing up the area of the square into four equal, smaller squares, making the big sides of the big square two units in length.

The area of the square is clearly 2×2 = 4:

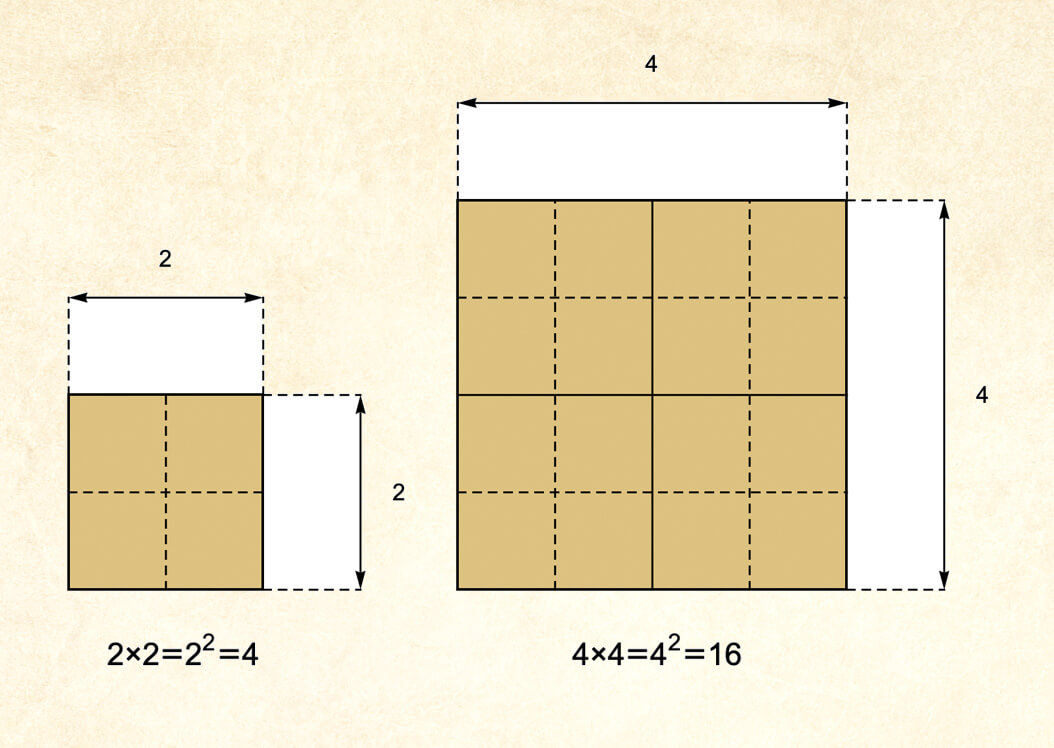
Socrates asked the boy to try and double the area of the square—to make the area 8 instead of 4. The boy was confident in his first answer: you would achieve this by doubling the length of the sides. Socrates helped the boy to see that the double sides don't actually produce a double square, but actually a quadruple square, with area 16!

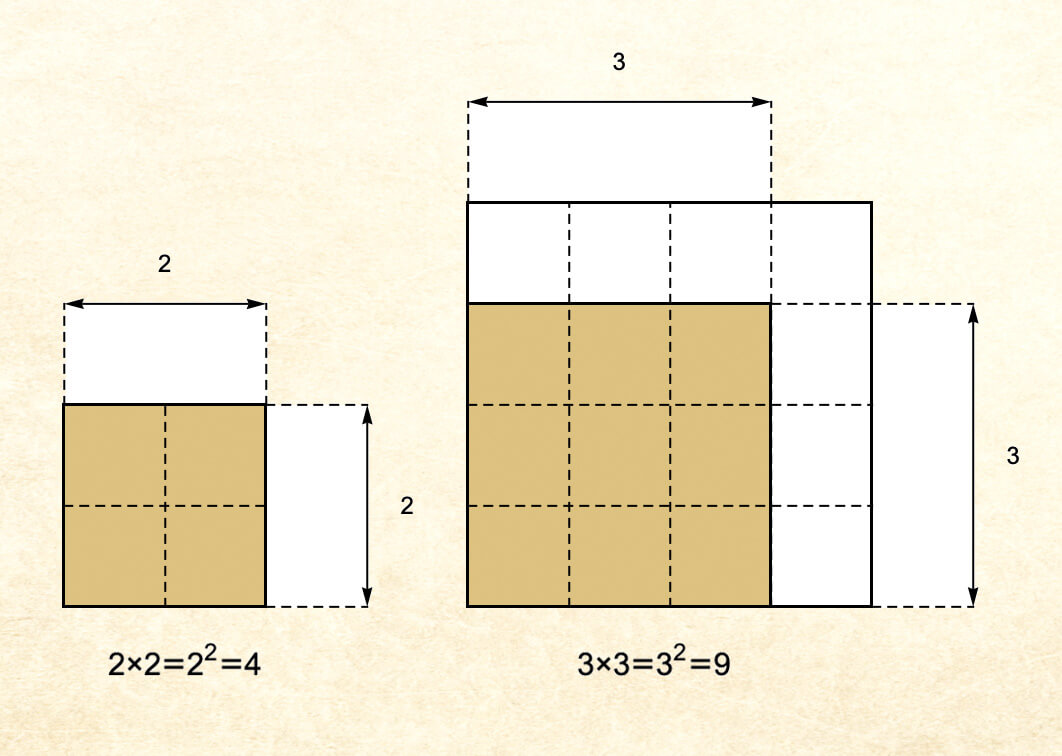
The boy tried again, and found that making a square with sides three units long wouldn't produce a double square either, but actually got a square with area 9:

At this point, the boy was frustrated, and wanted to give up. But then Socrates asked him a series of questions that guided him toward the correct answer, which is to use the diagonal of the original square as the base for the new square. Drag the slider for a proof that the shaded area is actually exactly twice as much as the original 2×2 square:

Socrates made lots of slightly strange conclusions from the boy's ability to work out the problem without being explicitly taught any math. His idea was that people know facts about the world from a past life, and learning is just remembering things you used to know.

Even if we don't agree with Socrates's conclusions on how people learn math, it's a good way of illustrating the kind of confusion that Bell would have felt as he tried to find a shape that let him keep the weight, surface area and volume in proportion even as the machine got big enough to support a person in the air.

Doubling the Volume of a Cube

Of course, Bell needed something a little more three-dimensional than a square. Let's see how the problem changes when we try to apply the method above to doubling the volume of a cube. Doubling the cube is one of the more famous problems of antiquity. It took mathematicians more than two thousand years to prove that the problem is actually impossible to solve using only a compass and a straightedge.

In order to double the volume of a cube, we'd need to do some impossible math.

Our first cube has sides with length 1. The formula for finding the volume is: volume = length × width × height, so if all the sides are 1, then the volume is 1 × 1 × 1 = 1.

In order to get a cube with volume 2, we'd need to find a number that, when you multiply it by itself three times (i.e. you cube it), you end up with the number 2.

The only number that works for this is the cube root of 2, :

Unfortunately, there's no way to construct a cube in real life with sides , as the number can't be constructed with a compass and a straightedge in a finite number of steps. In math, we say that numbers like this are not constructible numbers.

What if, like the boy with the square, we tried to double or triple the length of the sides of the cube? If the side's length is increased x times, then the surface and volume increase x² and x³ times, respectively. Look at this chart to see how much more quickly the volume increases than the surface area.

Let's look at this on some cubes and squares.

For Bell, this meant that when he was building his flying machine, shapes like the cube weren't possible, because building a machine big enough to carry a person would mean increasing the length, which would increase the volume and weight more rapidly than the surface area.

The Square-Cube Law

The square-cube law states what we just found out in a more mathematical way. Essentially, the surface area of a shape will increase by x², and the weight or volume of a shape will increase by x³, which is much larger.

This law made many people believe that making a flying machine was impossible—in order to be big enough to lift a person off the ground, it would be so heavy it wouldn't be able to fly.

Bell tried to make a lot of flying machines with cubes and other box shapes, but every time he tried, the square-cube law made it impossible. After a lot of failures and hard work, though, Bell discovered a mathematical principle ahead of his time, a result that now belongs to the mathematical field of fractal geometry.

He realized that he could use one of the five Platonic solids, the regular tetrahedron, as a building block. This shape would make his flying machines light and strong enough to lift a person off the ground.

Bell's trick consisted in nesting empty tetrahedra with two of the faces removed. Notice that the two-dimensional case generates a fractal known as the Sierpiński triangle. Keep adding more nesting to see how the bigger flying machines would look.

Using this shape, Bell discovered that his giant kites, even when they had hundreds of square feet of surface, remained proportional to the small kites he made. The shapes were really light in proportion to their surface areas.

Despite being three-dimensional objects, Bell's tetrahedral kites had fractal dimension 2. This is easily checked by looking at these kites from the bottom up. The kites will look like a perfect two-dimensional square since all face pairs from each tetrahedral cell will be fully visible.

Bell made several patents based on his mathematical discovery.

Bell went on to form a research group, the Aerial Experiment Association (AEA), to test different aircraft designs. In 1907, Bell's aircraft the Cygnet, constructed with 3,393 tetrahedral cells, made the first recorded heavier-than-air flight in Canada. Alexander Graham Bell's unique experimental designs were important in the history of early aviation.