History of Mathematics Project | Euclid Diagram Papyrus

History of
Mathematics

Project

around 75–125 CE

Euclid Diagram Papyrus

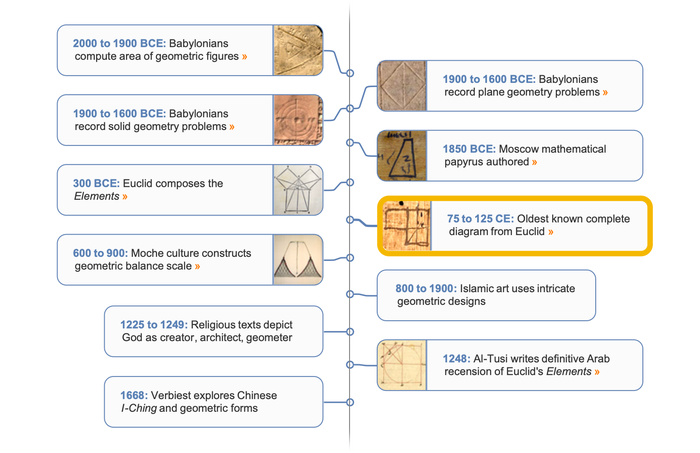
Oldest known complete diagram from Euclid's Elements

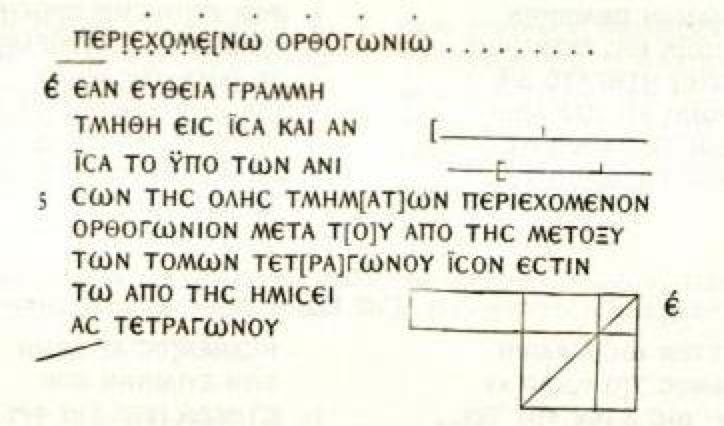
This fragment of a papyrus contains one of the oldest known complete diagrams from Euclid's Elements. It was discovered in Oxyrhynchus, Egypt, by an expedition of Grenfell and Hunt in 1896–1897.

The fragment contains an unlabeled diagram and a statement of the fifth proposition in Book 2 of the Elements: if a straight line be cut into equal and unequal segments, the rectangle contained by the unequal segments of the whole together with the square on the straight line between the points of section is equal to the square on the half. The statement can be interpreted as a geometric formulation of the algebraic identity (x + y)(x - y) + y² = x².

Artifact dimensions

8.5 cm × 15.2 cm

Original artifact location

Oxyrhynchus (historical name), Menia, Egypt (current name)

Current artifact location

Penn Museum, Philadelphia

Catalog number

E2748 (current), ES 2748 (historical)

Timeline

Interactive Content

Computational Explanation

The diagram on the papyrus reproduces the following figure from Book II, Proposition 5 in Euclid's Elements:

The proposition states, "If a straight line be cut into equal and unequal segments, the rectangle contained by the unequal segments of the whole together with the square on the straight line between the points of section is equal to the square on the half," and the preceding diagram provides a way to prove this result. To see the validity of the result, start with a line segment AB, cut it into equal segments AC and CD by placing C at the midpoint, and cut it into unequal segments by placing D between C and B:

Out[]=

The proposition then states:

AD·DB+CD·CDCB·CB

An algebraic proof follows immediately by labeling the distances in the preceding diagram:

Out[]=

by setting:

ACCBxCDy,

which gives:

ADx+yDBx-y.

Setting these up as rule replacements:

In[]:=

rules={ADx+y,CBx,CDy,DBx-y};

and plugging in:

In[]:=

ADDB+CDCDCBCB/.rules

Out[]=

+(x-y)(x+y)

Expanding the left-hand side, the equality is established:

In[]:=

Expand[

+(x-y)(x+y)]

Out[]=

This could also have been established all at once by plugging in and expanding at the same time:

In[]:=

Expand[ADDB+CDCDCBCB/.rules]

Out[]=

True

Rearranging the identity reveals the proposition as a geometric statement of the well-known algebraic identity:

(x+y)(x-y)=

Geometric proof of the proposition is somewhat more involved, but follows from a straightforward application of geometric reasoning based on properties of squares, rectangles and the gnomon CLHGFB. To prove the proposition geometrically, start with the line segment

, with

its midpoint and

on the line segment

In[]:=

linesegment=RandomInstance[GeometricScene[{"A"{0,0},"B"{10,0},"C","D"},{"C"Midpoint[Line[{"A","C","D","B"}]]}]]

Out[]=

Verify that the diagram so constructed satisfied the stated proposition:

In[]:=

With[{seg=EuclideanDistance},seg["A","D"]seg["D","B"]+seg["C","D"]seg["C","D"]seg["C","B"]seg["C","B"]]/.linesegment["Points"]

Out[]=

True

Now draw the square

CEFB

, and draw the line segment

. Draw the line segment

parallel to

, with

and with

intersecting

. Draw the line segments

and

, with

parallel to

, and with

parallel to

and intersecting

. To begin with, augment the line segment points with the points to be added:

points=Join[linesegment["Points"],{"E","F","G","H","K","L","M"}]

Out[]=

{A{0.,0.},B{10.,0.},C{5.,0.},D{6.699,0.},E,F,G,H,K,L,M}

Now use geometric assertions to construct the following picture, which corresponds to the papyrus diagram:

diagram=RandomInstance[GeometricScene[points,{GeometricAssertion[{Line[{"A","B"}],Line[{"K","L","H","M"}]},"MatchingParallel"],GeometricAssertion[Polygon[{"C","E","F","B"}],"Regular"],Line[{"B","H","E"}],Line[{"E","G","F"}],Line[{"B","M","F"}],GeometricAssertion[{Line[{"D","H","G"}],Line[{"C","L","E"}],Line[{"A","K"}]},"MatchingParallel"]}]]

Out[]=

Again extract the points, which now have explicit coordinates based on their construction:

points=Cases[diagram["Points"],HoldPattern[_String_]];

Note that

equals

since

DHMB

is a square, and that

LEGH

is a square whose sides are equal to

, so the proposition states that the area of rectangle

AKHD

plus the area of square

LEGH

equals the area of square

CEFB

. We prove this statement in the following series of steps.

Since the rectangle

CLHD

equals the rectangle

HGFM

, adding the square

DHMB

to each shows that the rectangle

CLMB

equals the rectangle

DGFB

In[]:=

RandomInstance[GeometricScene[points,{Line[{{"C","A"},{"A","K"},{"K","L"},{"L","E"},{"E","G"},{"E","B"}}],Style[Polygon[{"C","L","M","B"}],Orange],Style[Polygon[{"D","G","F","B"}],Blue]}]]

Out[]=

The rectangle

AKLC

equals the rectangle

CLMB

, since

equals

and

equals

, so it also equals the rectangle

DGFB

. Adding the rectangle

CLHD

to both

AKLC

and

DGFB

shows that rectangle

AKHD

and gnomon

CLHGFB

have the same area:

In[]:=

RandomInstance[GeometricScene[points,{Line[{{"C","A"},{"A","K"},{"K","L"},{"L","E"},{"E","G"},{"E","B"},{"H","M"}}],Style[Polygon[{"A","K","H","D"}],Orange],Style[{Polygon[{"C","L","H","D"}],Polygon[{"D","G","F","B"}]},Blue]}]]

Out[]=

Adding the square

LEGH

to the gnomon

CLHGFB

gives the square

CEFB

, so also adding

LEGH

to the rectangle

AKHD

shows that the area of

AKHD

plus the area of

LEGH

equals the area of

CEFB

, as desired:

In[]:=

RandomInstance[GeometricScene[points,{Line[{{"C","A"},{"A","K"},{"K","L"},{"L","E"},{"E","G"},{"E","B"},{"H","M"}}],Style[{Polygon[{"A","K","H","D"}],Polygon[{"L","E","G","H"}]},Orange],Style[{Polygon[{"C","E","F","B"}]},Blue]}]]

Out[]=

Other Resources

History of Mathematics
Euclid's Elements

Additional Reading

Fowler, D. The Mathematics of Plato's Academy, 2nd ed. Oxford, England: Clarendon Press, 1999.
Euclid. Euclid's Elements. Green Lion Press, 2002.
Grenfell, B. P. and Hunt, A. S. Plate 58 in Oxyrhynchus Papyri I, Vol. IV. London: Egypt Exploration Fund, 1898.
Heath, T. L. Euclid's Elements, Vol. 1 (Books I and II). New York: Dover, 1956.

Additional Links

Image Credits

Wikimedia

Euclid Diagram Papyrus

Timeline

Interactive Content

Computational Explanation

Other Resources

History of Mathematics

Wolfram MathWorld

Additional Reading

Additional Links

Image Credits