History of Mathematics Project | Sumerian 7 Quotient and 10 Product Tablet

History of
Mathematics

Project

around 1900–1600 BCE

Sumerian 7 Quotient and 10 Product Tablet

Reciprocals and multiplication by 7 and 10 in cuneiform

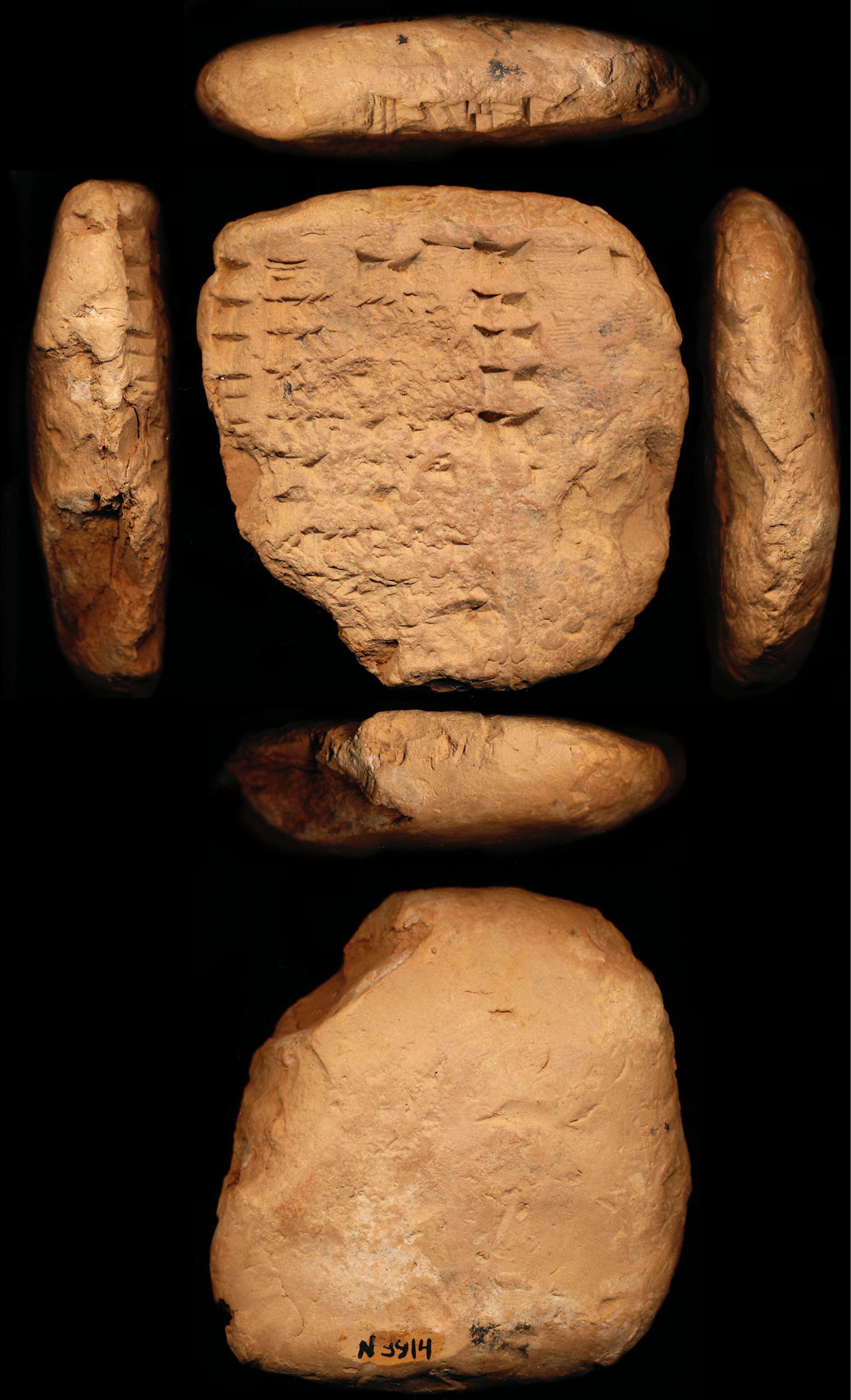
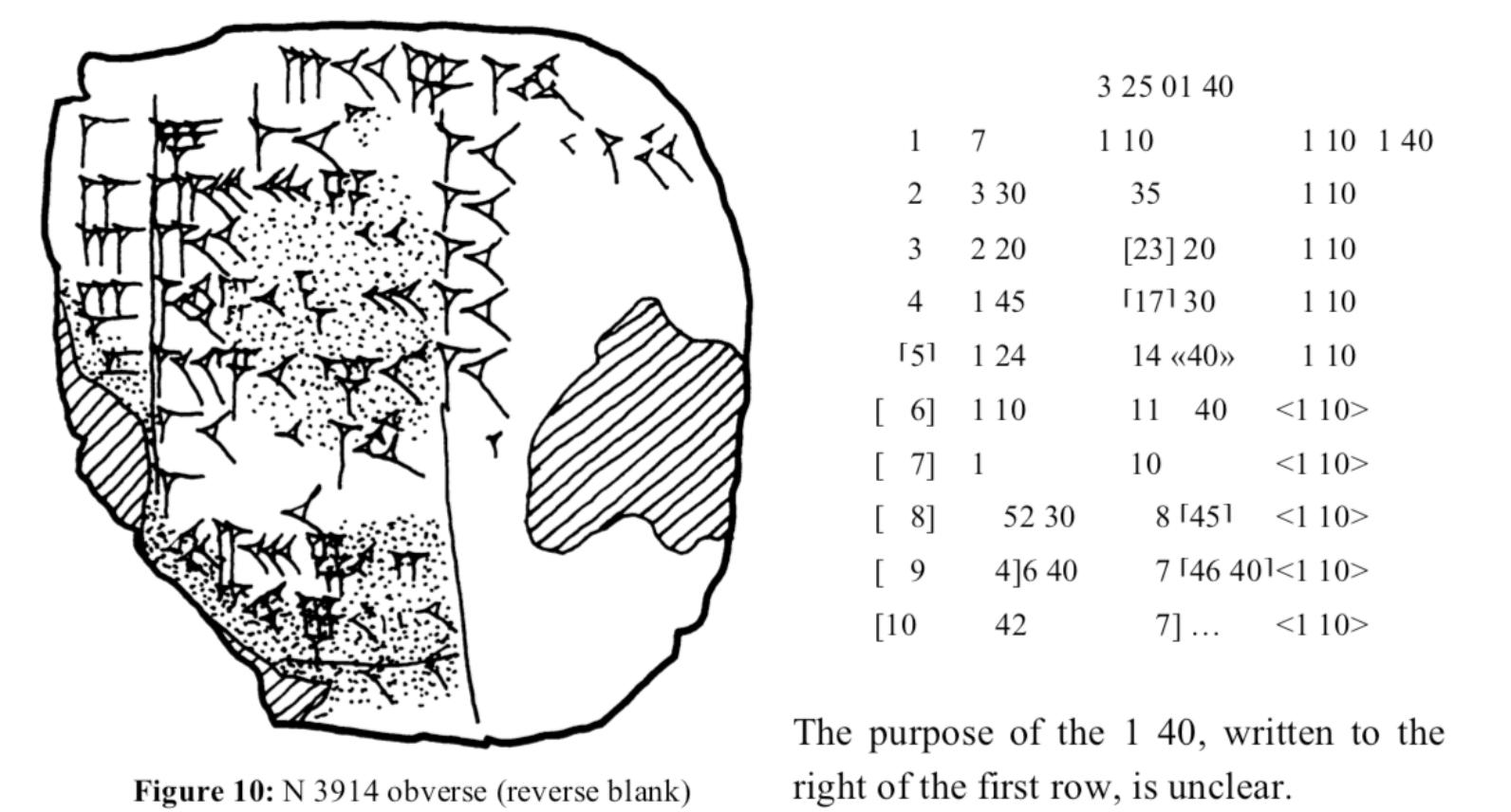
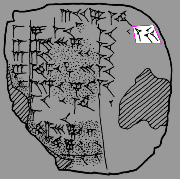
Many mathematical Babylonian tablets contain tables of divisions or multiplications. Tablet N3914, held by the Penn Museum in Philadelphia, tabulates 7/n and a number of products involving those quotients for integers n from 1 to 10. All are written in the base 60, or sexagesimal, number representation used by the Babylonians.

Sumerian 7 Quotient and 10 Product Tablet

This old Babylonian tablet contains division and multiplication calculations laid out in a tabular format. The first column of the table is a simple count of the integers 1 to 10, though the numbers 5–10 are partially or completely missing. The second column gives 7 divided by the numbers in the first column, while the third column gives the numbers in the second column multiplied by 10. The fourth and final column gives the products of the first and third columns which, because n × (7/n × 10), is always the number 70, written in base-60 numbers as 1 10, i.e. 1 × 60 + 10 × 1. The number at the top of the third column is the sum of the numbers in that column. The significance of an additional number written at the end of the first row is not known.

Artifact dimensions

7 in. × 7 in. × 2 in.

Original artifact location

Nippur (historical name), Afak, Al-Qadisiyah, Iraq (current name)

Current artifact location

Penn Museum, Philadelphia

Catalog number

N3914

Timeline

Interactive Content

Computational Explanation

Tablet N3914 is held by the Penn Museum in Philadelphia and dated to 1900–1600 BCE. It originates from the ancient Babylonian city of Nippur and contains division and multiplication calculations laid out in a tabular format starting with the numbers 1–10. The following figure illustrates the original together with a schematic of its numeric markings drawn by Robson (2000):

Out[]=

Unlike our base 10 system for representing numbers, the Babylonian system of numeration consisted of base 60 numbers written in cuneiform script. The following table summarizes cuneiform representations of the whole numbers 1 to 40:

In[]:=

TextGridFlatten/@TransposePartitionTablen,

[◼]	AncientNumberRepresentation

[n,"Babylonian"],{n,40},10,DividersAll

Out[]=

1	11	21	31
2	12	22	32
3	13	23	33
4	14	24	34
5	15	25	35
6	16	26	36
7	17	27	37
8	18	28	38
9	19	29	39
10	20	30	40

The preserved part of the first column clearly contains the numbers 1–4 written in cuneiform.

Quotient and Product Table

The first column of the table is a simple count of the integers 1 to 10, though the portion of the tablet containing half of the number 5 and all of the numbers 6–10 is lost. The second column gives 7 divided by the numbers in the first column, while the third column gives the numbers in the second column multiplied by 10. The fourth and final column gives the products of the first and third columns. The value in the last column is therefore given by n × (7/n × 10), which is always 70.

Performing these computations in familiar base 10 gives the following table:

In[]:=

TextGrid[Table[{n,7/n,70/n,70},{n,10}]]

Out[]=

1	7	70	70
2	7 2	35	70
3	7 3	70 3	70
4	7 4	35 2	70
5	7 5	14	70
6	7 6	35 3	70
7	1	10	70
8	7 8	35 4	70
9	7 9	70 9	70
10	7 10	7	70

In order to view the computations in sexagesimal, define a simple function to convert and display a number in base 60:

In[]:=

sexigesimalDigits[n_?NumericQ]:=Row[RealDigits[n,60][[1]],Spacer[2]]

Now perform the computations and display them beside a transcription from Robson (2000):

In[]:=

table=TextGrid[Table[Thread[sexigesimalDigits[{n,7/n,70/n,70}]],{n,10}],Spacings{1,1.1},BaseStyle18];

Out[]=

Computing the first three rows and displaying in cuneiform:

GridMap

[◼]	AncientNumberRepresentation

[#,"Babylonian"]&,Table[{n,7/n,70/n,70},{n,3}],{2},AlignmentLeft

… also shows good agreement with the original:

Out[]=

Why 7/n Is Special

It is notable that this table contains quotients of 7. This is no chance choice, but follows from the fact that unit fractions are expressible in closed form using a given base b if their denominators contain only factors of b. For example, in our familiar base-10 system,

102×5

, so the fractions like 1/2  0.5, 1/4  0.25 and 1/5  0.2 have finite expansions, whereas fractions like 1/3  0.333… and 1/7  0.142… do not. Similarly, in base 60, the denominators of terminating fractions contain only factors of:

In[]:=

FactorInteger[60][[All,1]]

Out[]=

{2,3,5}

… or else the trivial factor 1.

A sequential table of the first 20 positive unit base-60 fractions will therefore fail to terminate for the following values:

In[]:=

Select[Range[20],!ContainsOnly[FactorInteger[#][[All,1]],{1,2,3,5}]&]

Out[]=

{7,11,13,14,17,19}

However, if the range is restricted to the first 10 positive numbers and, instead of 1/n, 7/n is used, then 7/7  1, so all quotients in the table can be written exactly:

In[]:=

Select[Range[10],!ContainsOnly[FactorInteger[Denominator[7/#]][[All,1]],{1,2,3,5}]&]

Out[]=

{}

While there do exist Babylonian tablets that contain approximate expansions of non-terminating base-60 fractions (notably tablet YPM BC 024321 from the Yale University Babylonian Collection), most tablets prefer to avoid fractions that are not finitely expressible.

Column Sum Header

The number at the top of the third column:

Out[]=

… is the sum of the numbers in that column, namely the sum of 70k for k = 1 to 10:

In[]:=

Total[Table[70/n,{n,10}]]

Out[]=

7381

Sums of consecutive integer reciprocals have a closed form in terms of a special function called the harmonic number:

In[]:=

Sum[1/n,{n,k}]

Out[]=

HarmonicNumber[k]

… so the sum can be immediately computed in the Wolfram Language as:

In[]:=

70HarmonicNumber[10]

Out[]=

7381

In sexagesimal, the sum has digits 3 25 1 40  3 × 60 + 25 × 1 + 1/60 + 40/60²:

In[]:=

RealDigits

7381

,60//First

Out[]=

{3,25,1,40}

In cuneiform, that sum becomes the sequence of digits observed at the top of the tablet:

In[]:=

Row

[◼]	AncientNumberRepresentation



7381

,"Babylonian"

Out[]=

Row



Mystery Number at the End of Row 1

The meaning of the digits 1 40 written to the right of the first row is unclear:

Out[]=

In[]:=

Row

[◼]	AncientNumberRepresentation

[{1,40},"Babylonian"]

Out[]=

One possible interpretation is as the square of the number of rows, i.e.

100

In[]:=

[◼]	AncientNumberRepresentation

[100,"Babylonian"]

Out[]=

However, since the Babylonian numeration system did not use place values, it could also mean any power of 60 times that number:

In[]:=

Table[100

,{n,-3,3}]

Out[]=



2160

,100,6000,360000,21600000

Other Resources

History of Mathematics
Babylonian Reciprocals Tablet

History of Mathematics
Babylonian Scribe School Multiplication Tablet

Wolfram Demonstration
Babylonian Numerals

Wolfram Demonstration
Multiplication Table

Additional Reading

Cajori, F. A History of Mathematical Notations: Two Volumes Bound as One, Vol. 1. New York: Dover, pp. 2–4, 1928.
Robson, E. Fig. 10 in "Mathematical Cuneiform Tablets in Philadelphia, Part 1: Problems and Calculations." SCIAMVS, Vol. 1, pp. 11–48, 2000.

Additional Links

Cuneiform Digital Library Initiative: P278884

Image Credits

Penn Museum

1	11	21	31
2	12	22	32
3	13	23	33
4	14	24	34
5	15	25	35
6	16	26	36
7	17	27	37
8	18	28	38
9	19	29	39
10	20	30	40

1	11	21	31
2	12	22	32
3	13	23	33
4	14	24	34
5	15	25	35
6	16	26	36
7	17	27	37
8	18	28	38
9	19	29	39
10	20	30	40

Sumerian 7 Quotient and 10 Product Tablet

Timeline

Interactive Content

Computational Explanation

Quotient and Product Table

Why 7/n Is Special

Column Sum Header

Mystery Number at the End of Row 1

Other Resources

History of Mathematics

History of Mathematics

Wolfram Demonstration

Wolfram Demonstration

Additional Reading

Additional Links

Image Credits

1	11	21	31
2	12	22	32
3	13	23	33
4	14	24	34
5	15	25	35
6	16	26	36
7	17	27	37
8	18	28	38
9	19	29	39
10	20	30	40