History of Mathematics Project | Ptolemy's Quadrilateral Theorem

History of
Mathematics

Project

around 150 CE

Ptolemy's Quadrilateral Theorem

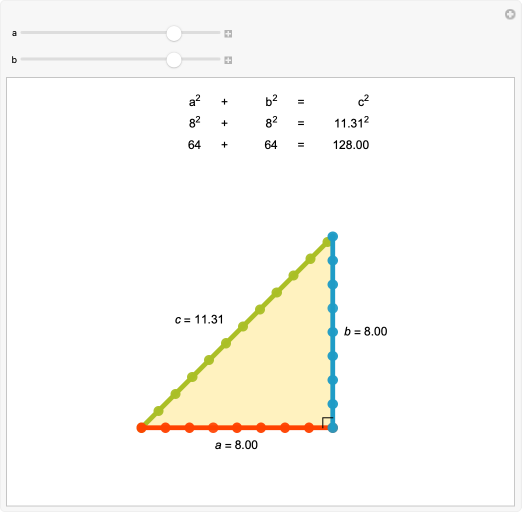
The Pythagorean theorem via cyclic quadrilaterals

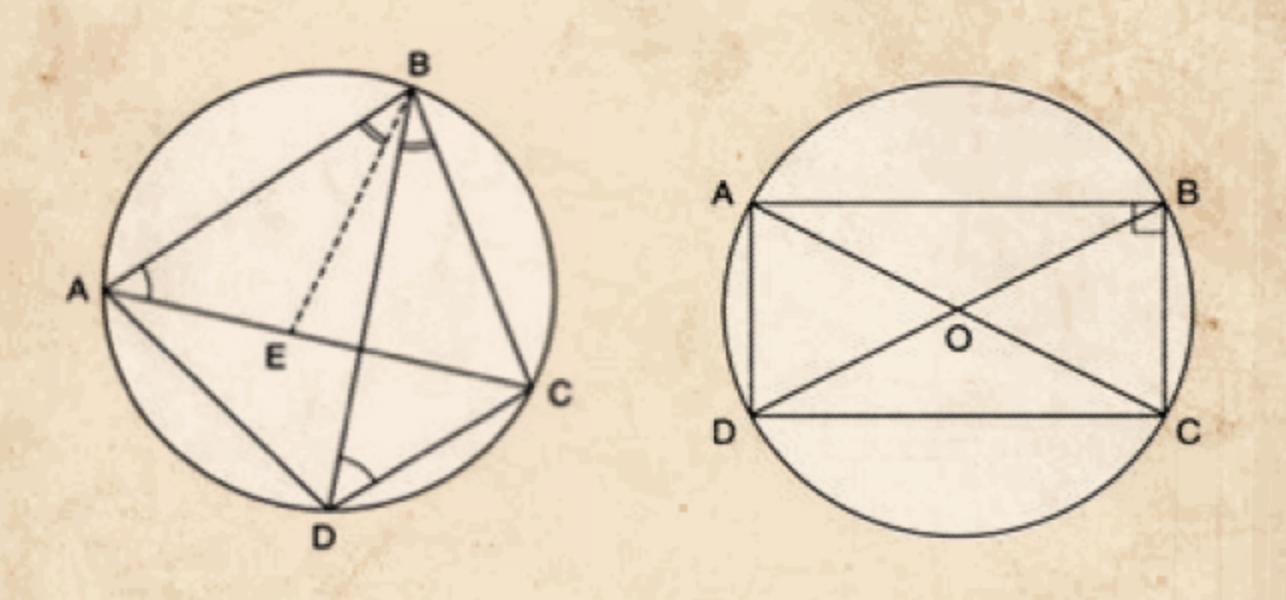
Claudius Ptolemy's famous work the Almagest gives a result on cyclic quadrilaterals, which gives the Pythagorean theorem as a special case.

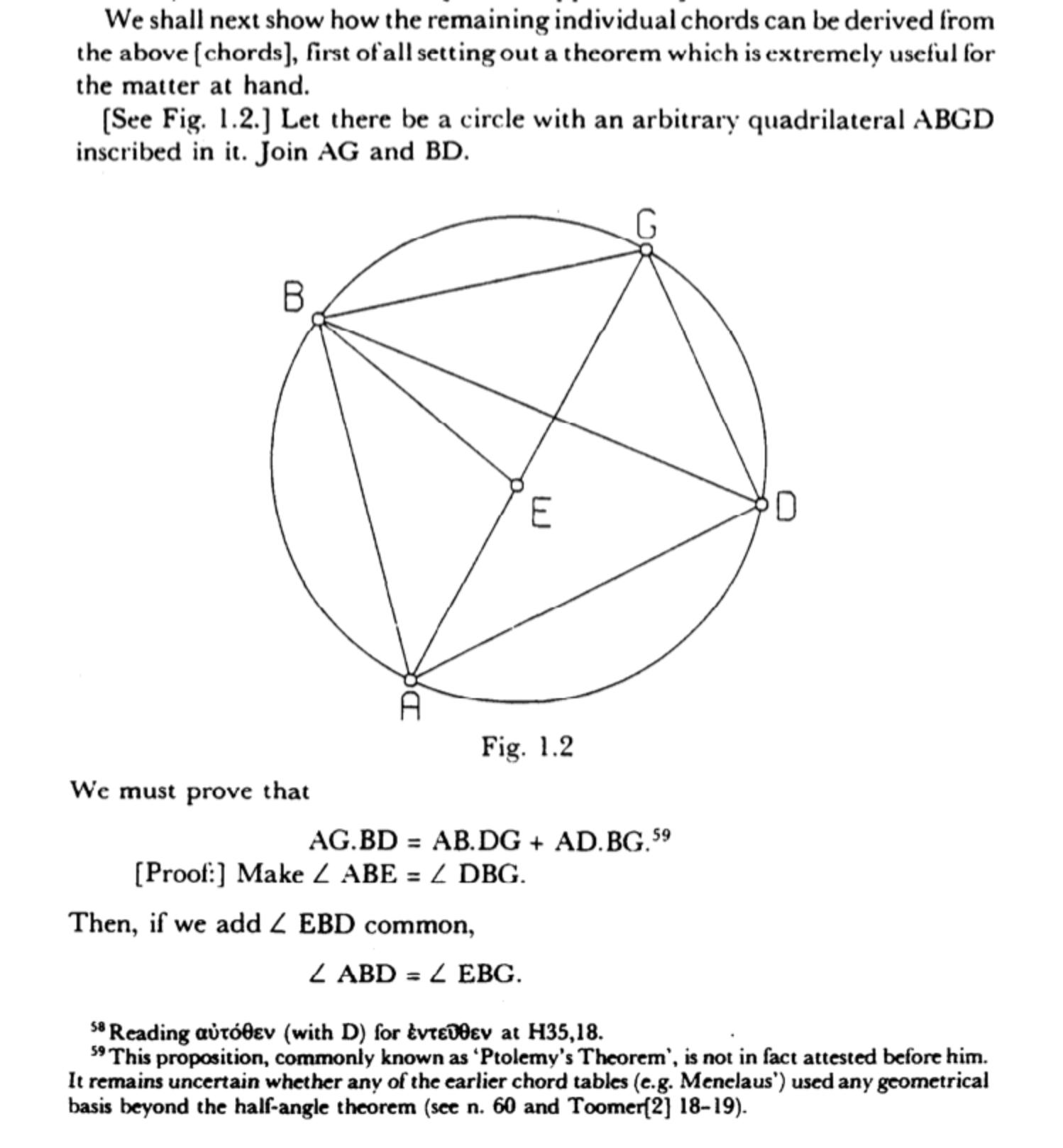
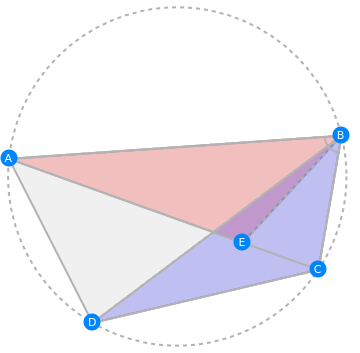
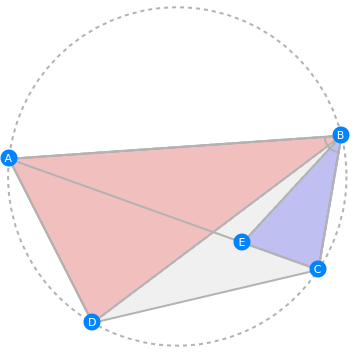
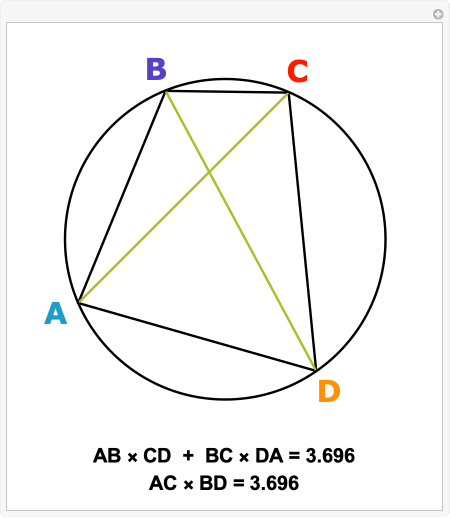
Book 1, Chapter 10 of the Almagest contains a relation between the sides and diagonals of a cyclic quadrilateral known as Ptolemy's theorem: AB×CD + BC×DA = AC×BD. Taking the special case of the quadrilateral being a rectangle, this result reduces to the Pythagorean theorem, thus providing one of the world's first alternate proofs.

Artifact format

Unknown (lost)

Artifact origin

Alexandria, Egypt

Timeline

Interactive Content

Computational Explanation

Ptolemy's theorem states that for a cyclic quadrilateral

ABCD

AB×CD+BC×DAAC×BD

We draw a random instance of a cyclic quadrilateral:

In[]:=

scene=RandomInstance[GeometricScene[{"A","B","C","D"},{GeometricAssertion[Polygon[{"A","B","C","D"}],"Cyclic"]}]]

Out[]=

We confirm that Ptolemy's theorem holds in this instance:

{EuclideanDistance["A","B"]EuclideanDistance["C","D"]+EuclideanDistance["B","C"]EuclideanDistance["D","A"],EuclideanDistance["A","C"]EuclideanDistance["B","D"]}/.scene["Points"]

Out[]=

{6.63127,6.63127}

To see why Ptolemy's theorem holds in general, we add the point

found in the visual proof from the Almagest and set

as the point on the diagonal

such that

∠ABE

and

∠CBD

are equal:

In[]:=

points=Append[Cases[scene["Points"],HoldPattern[Alternatives["A","B","C","D"]_]],"E"];RandomInstance[GeometricScene[points,{GeometricAssertion[Polygon[{"A","B","C","D"}],"Cyclic"],Line[{"A","E","C"}],PlanarAngle[{"A","B","E"}]PlanarAngle[{"C","B","D"}]}]]

Out[]=

In[]:=

RandomInstance[GeometricScene[points,{GeometricAssertion[Polygon[{"A","B","C","D"}],"Cyclic"],Line[{"A","E","C"}],PlanarAngle[{"A","B","E"}]PlanarAngle[{"C","B","D"}],Style[Triangle[{"A","B","E"}],Red],Style[Triangle[{"D","B","C"}],Blue]}]]

Out[]=

Note that

∠ABD

and

∠CBE

are equal, since

∠ABE

and

∠CBD

are equal, and

∠DBE

is the common difference between

∠ABE

and

∠ABD

as well as between

∠CBD

and

∠CBE

. Since

∠ADB

and

∠BCE

subtend the same arc, they are also equal. Thus

△ABD

and

△EBC

are similar, so



, or

BC×DAEC×BD

In[]:=

Out[]=

Adding these equations together, we get

AB×CD+BC×DAAE×BD+EC×BDAC×BD

, as desired. Note that in the case of a rectangle

ABCD

, this reduces to the Pythagorean theorem, as

ABCD

BCDA

and

ACBD

In[]:=

RandomInstance[GeometricScene[{"A","B","C","D"},{GeometricAssertion[Polygon[{"A","B","C","D"}],"Cyclic","Equiangular"],Style[Triangle[{"A","B","C"}],Red]}]]

Out[]=

So:

A

Other Resources

Wolfram Demonstration
Pythagorean Theorem

Additional Reading

Coolidge, J. L. "A Historically Interesting Formula for the Area of a Quadrilateral." Amer. Math. Monthly, Vol. 46, pp. 345–347, 1939.
Coxeter, H. S. M. and Greitzer, S. L. "Ptolemy's Theorem and Its Extensions." §2.6 in Geometry Revisited. Washington, DC: Mathematical Association of America, pp. 42–43, 1967.
Durrell, C. V. and Robson, A. Advanced Trigonometry. p. 25, 1930.
Johnson, R. A. "The Theorem of Ptolemy". §92 in Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, pp. 62–63, 1929.
Kimberling, C. "Triangle Centers and Central Triangles." Congr. Numer., No. 129, p. 223, 1998.
Maor, E. The Pythagorean Theorem: A 4000-Year History. Princeton, NJ: Princeton University Press, pp. 104–105, 2007.
Ptolemy, C. Almagestum. Latin translation of Gerard of Cremona. Venice, Italy: Petrus Lichtenstein, left leaf of p. 6, 1515.
Toomer, G. J. Ptolemy's Almagest. Princeton, NJ: Princeton University Press, 1988.
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 200–201, 1991.