Timeline

Interactive Content

Use the following controls to construct a woven balance scale in which nested triangular patterns are created using bunches of equally spaced strands:

Out[]=

​
bunch count 1 2 3 4 5 strand count 1 2 3 4 5 strand separation net opening angle additional parameters

Computational Explanation

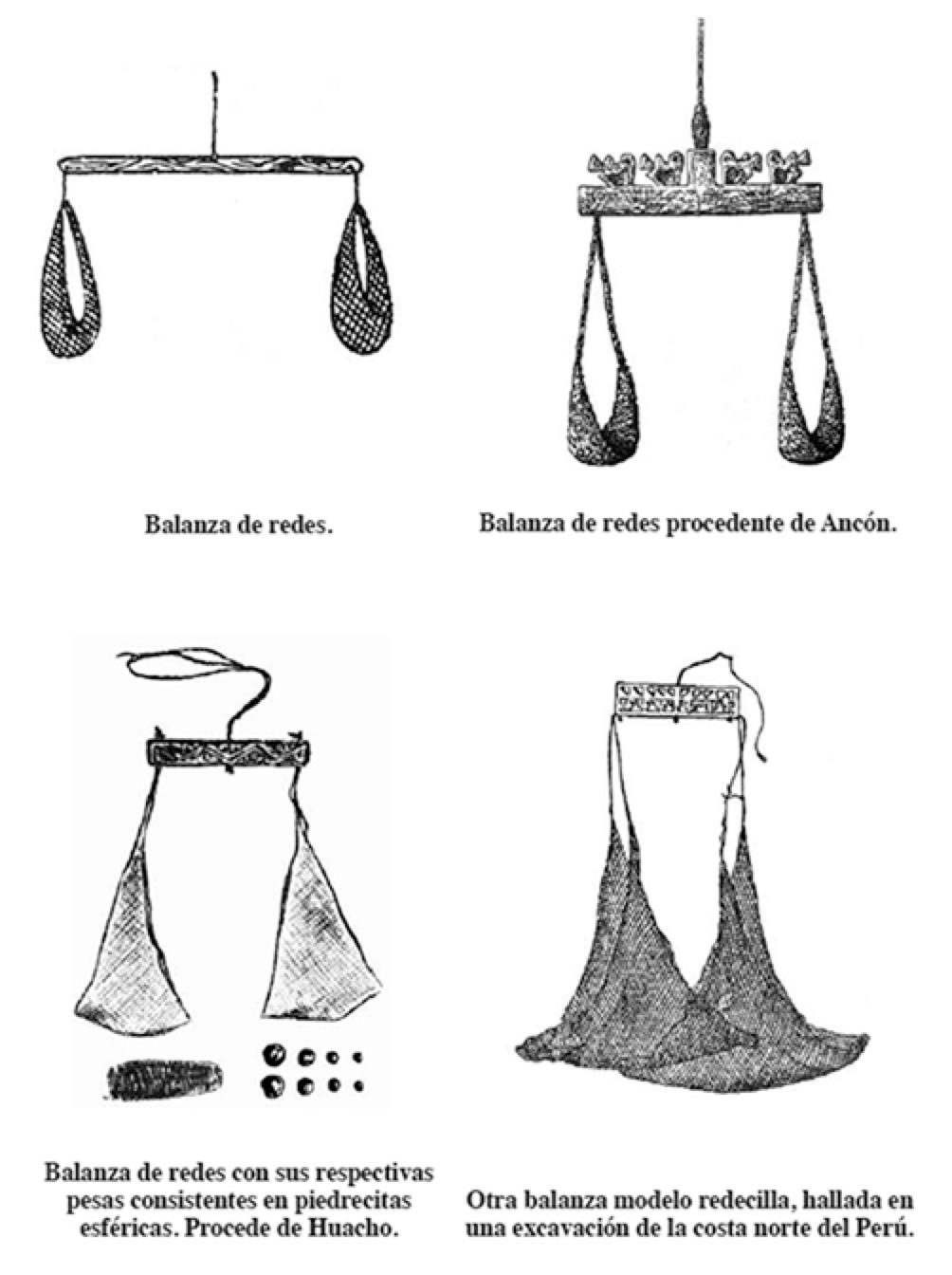
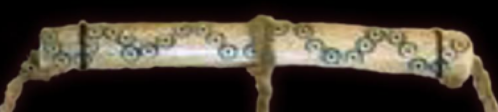
This net balance scale originates from pre-Columbian Peru around 600–900 CE. It features two woven diamond-shaped nets made of wool, cotton and linen suspended to create a triangular form with a nested geometric diamond pattern of threads. The balance contains multi-ply yarn, which was uncommon in Moche culture, suggesting it was used to weigh materials of high value. The similar but less ornate balance scale held by the Emory University Michael C. Carlos Museum is presumably more typical of those used by the Moche:

The balance beam of the scale is decorated with a connected trail of dots in circles:

The dotted circle is an ancient symbol also known as a circled dot or circumpunct. The circled dot motif may have been viewed as having magical significance, possibly as an abstract symbol to ward off the evil eye. The dotted circle can be easily constructed with a simple tool and is found in many cultures across historical periods; see for example the Islamic pawn chess piece dating from the 8th–11th centuries held by the Metropolitan Museum of Art and the ceramic vessel depicted in a study by Ziolkowski and Al-Sharqi (2006):

Ancient peoples inscribed or painted chains of circled dots by hand, often resulting in circles of equal radius but often with deviations from regular positioning and other imperfections. Using a single line of Wolfram Language code and the built-in function FindRoot, it is possible to construct perfectly aligned chains in which the circles are centered exactly on a desired curve and adjacent circles are exactly tangent to one another:

In[]:=

NextCircle[Circle[{x0_,y0_},r_],f_]:=Module[{x,y},Circle[{x,y},r]/.FindRoot[{(x-x0)^2+(y-y0)^2(2r)^2,f[x]y},{x,x0+r},{y,y0}]]

To apply the preceding function, start with a circle

c

1

and apply NextCircle to it to obtain

c

2

along the sine curve

ysinx

:

In[]:=

c1=Circle[{0,0},.2];​​c2=NextCircle[c1,Sin]

Out[]=

Circle[{0.284753,0.28092},0.2]

Now define a utility function to draw a dotted (instead of a plain) circle:

In[]:=

DottedCircle[ctr_,r_]:={Circle[ctr,r],AbsolutePointSize[5],Point[ctr]}

… and plot

c

1

and

c

2

together with the curve

ysinx

to confirm two tangent circles with centers on the desired curve have been constructed:

In[]:=

Show[Plot[Sin[x],{x,0.,1}],Graphics[{c1,c2}/.CircleDottedCircle],AxesTrue,AspectRatio->Automatic]

Out[]=

The process is then easily repeated to obtain a sequence of tangent circles:

In[]:=

CircleChain[c_Circle,f_,xmax_]:=NestWhileList[NextCircle[#,f]&,c,#[[1,1]]+#[[2]]<=xmax&]

In[]:=

DottedCircleChain[c_Circle,f_,xmax_]:=Module[{circles=CircleChain[c,f,xmax]},{circles,Point[circles[[All,1]]]}]

This function can then be applied to one period of a sine curve:

In[]:=

Show[Plot[Sin[x],{x,0,2Pi}],Graphics[DottedCircleChain[c1,Sin,2Pi]],AxesTrue,AspectRatio->Automatic,PlotRange->All]

Out[]=

… several periods of a triangle wave:

In[]:=

Show[Plot[2TriangleWave[x/4],{x,0,10}],Graphics[DottedCircleChain[c1,2TriangleWave[#/4]&,10]],AxesTrue,AspectRatio->Automatic,PlotRange->All]

Out[]=

… or any other continuous function that varies sufficiently slowly.

Placing a chain of circles inside a rectangle then gives a pattern resembling the beam of the Moche balance:

In[]:=

Module{bw=1,bh=.1,periods=4,dotR=.03,f},​​f[x_]:=(bh-dotR)Sinperiods

x

bw-dotR

+1π;​​Graphics[{​​FaceForm[LightYellow],EdgeForm[Black],​​Rectangle[{-bw,-bh},{bw,bh}],​​Darker@Blue,​​DottedCircleChain[Circle[{dotR-bw,f[dotR-bw]},dotR],f,bw-dotR]​​}]

Out[]=

Constructing nested triangles corresponding to the woven baskets on either side of the balance is an exercise in simple geometry and trigonometry. Allowing b clusters of threads with s strings in each cluster and plotting the results for

b,s1,…,4

gives the following set of attractive nested triangle "nets" resembling those in the original balance scale:

In[]:=

cs[q_]:=Through[{Cos,Sin}[q]];​​GraphicsGridTableWith{bL=1.5,ϕ=30},Module{ds=.06,w=bLSin[ϕDegree],h=bLCos[ϕDegree],x,y,dx},​​Graphics​​{AbsoluteThickness[3],Table[{If[Mod[i,2]0,Black,Red],Line[{cs[-π/2-kϕDegree]bLi/5,cs[-π/2-kϕDegree]bL(i+1)/5}]},{i,0,4},{k,{-1,1}}]},​​TableLine{x,y}=-{w,h}+

2wi

b+1

,0+j-

s+1

2

ds,0;dx=

ds

2w

j-

s+1

2

;{x,y}+

i

b+1

+dxbLcs

π

2

+ϕDegree,{x,y},{x,y}+1-

i

b+1

-dxbLcs

π

2

-ϕDegree,{i,b},{j,s},{b,4},{s,4},ImageSizeMedium

Out[]=

Adding two nets suspended on either side of the central beam together with some other small embellishments then gives a schematic representation of the Moche balance scale:

Additional Reading

• Smith, D. A. and Spier, L. "The Dot and Circle Design in Northwestern America." Journal de la société des américanistes Année, Vol. 19, p. 47–55, 1927.
• Hernandez, J.; Maloney, M.; and Flores, A. "Net Balance Scale." [link]
• Hoffmann, C. A. "El juego de chuncana entre los chimú. Un tablero de madera que prueba la hipótesis de Erland Nordenskiöld." Bulletin de l'Institut Français d'Études Andines, Vol. 32, Issue 2, pp. 317–345, 2003.
• O'Neale, L. M. "A Note on Certain Mochica (Early Chimu) Textiles." American Antiquity, Vol. 12, pp. 239–245, 1947.
• Thompson, D. "An Aesthetically Functional Set of Ancient Andean Fiberwork Scales at the Michael C. Carlos Museum, Emory University, Atlanta." Ars Textrina, Vol. 21, pp. 85–106, June 1994.
• Thompson, D. "Ancient Andean Textiles: A Balancing Act." Fiberarts, Vol. 22, No. 2, p. 16, Sept./Oct. 1995.
• Ziolkowski, M. C. and Al-Sharqi, A. S. "Dot-in-Circle: An Ethnoarchaeological Approach to Soft-Stone Vessel Decoration." Arabian Archaeology and Epigraphy, Vol. 17, Issue 2, pp. 152–162, 2006.

Additional Links

• Collections Database: Five Colleges and Historic Deerfield Museum Consortium: Net Balance Scale
• Dumbarton Oaks Research Library and Collection: Pre-Columbian Collection: Balance-Beam Scale
• Emory University Michael C. Carlos Museum: Set of Fiber Scales on Wood Beam
• The Metropolitan Museum of Art: Chess Piece, Pawn
• OER Commons: Math, Grade 6 Equations and Inequalities Symbolic Representation
• Wikipedia: Andean textiles
• Wikipedia: Moche culture