attributed to 200–300 CE
Liu Hui's Exhaustion Method
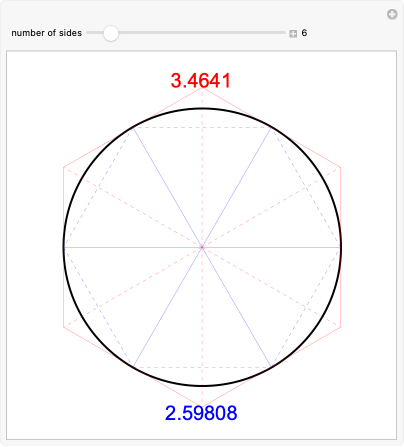
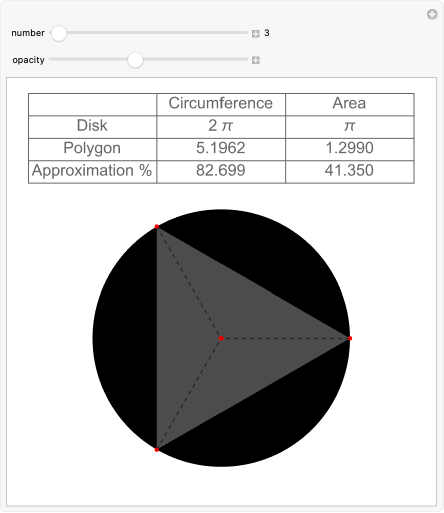
Using recursively inscribed polygons to approximate π
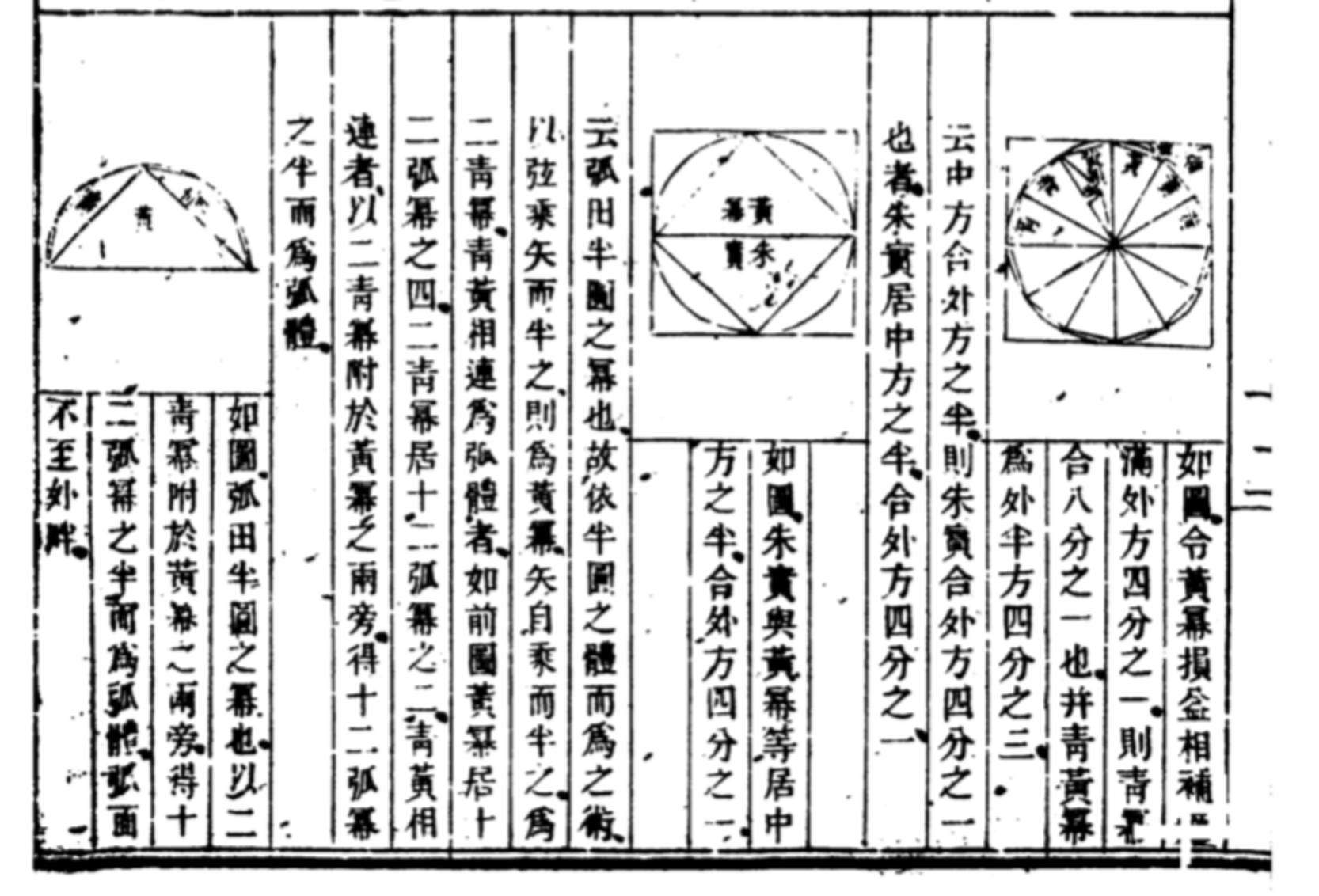
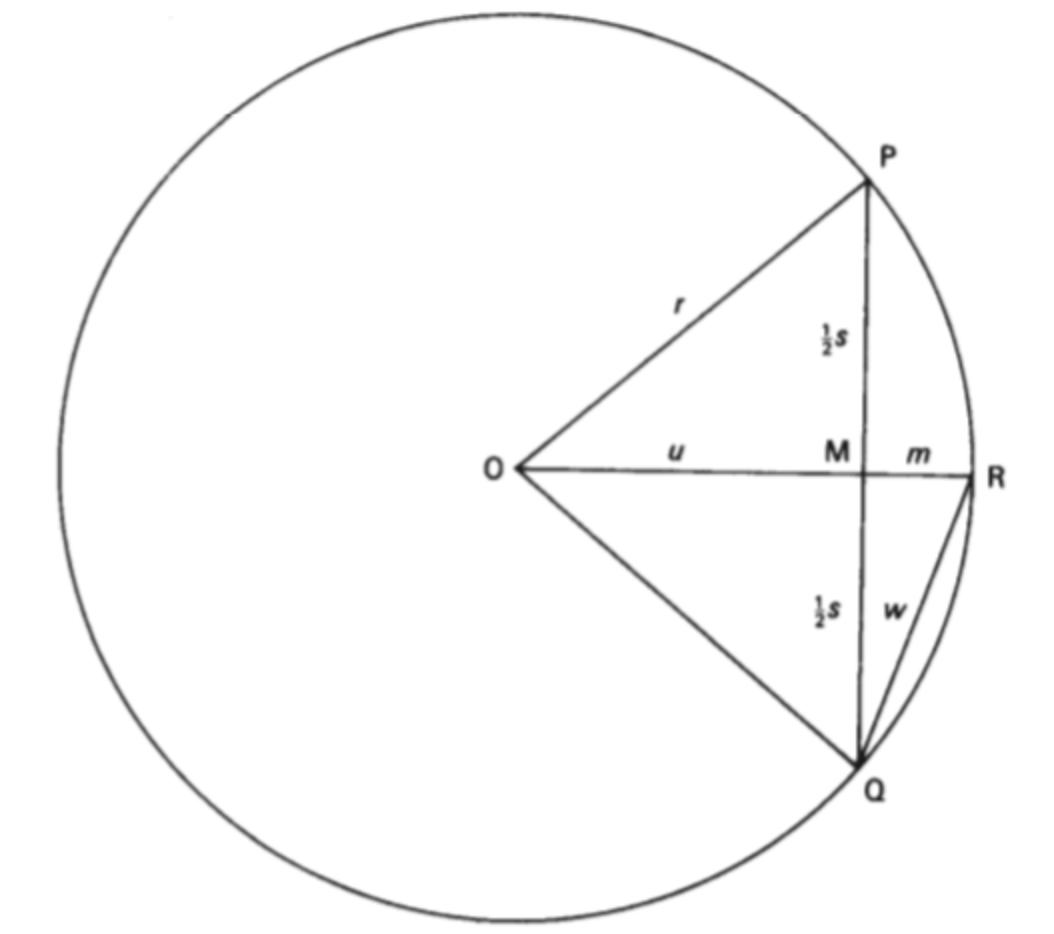
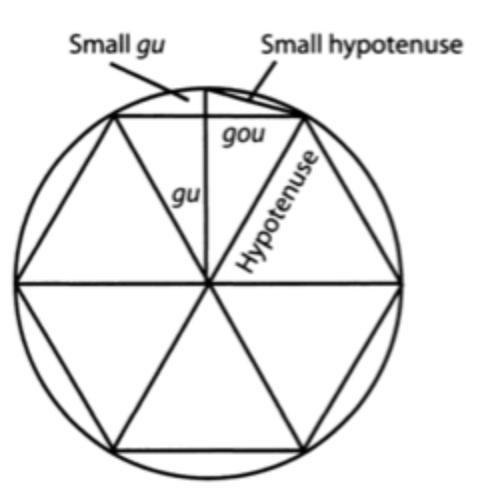
A commentary prepared by Chinese mathematician Liu Hui around 300 CE used a clever method of exhaustion based on the Pythagorean theorem for determining the area of a disk and estimating the value of π.

This page from a sixteenth-century Ming dynasty edition of Jiuzhang suanshu (The Nine Chapters on the Mathematical Art) illustrates the method of exhaustion for determining the area of a disk. While no copies of the original work survive, it is preserved through extant copies of an edition and commentary prepared by Liu Hui around 300 CE. By inscribing regular polygons in a circle and computing their areas using a recursive procedure based on the areas of the "kites" made from pairs of triangles, Liu proved that 3.14103 < π < 3.14271 and gave an accurate estimate of the actual value as π = 3927/1250 = 3.1416.