History of Mathematics Project | Hermes's Suitcase of Göttingen

History of
Mathematics

Project

1884–1894

Hermes's Suitcase of Göttingen

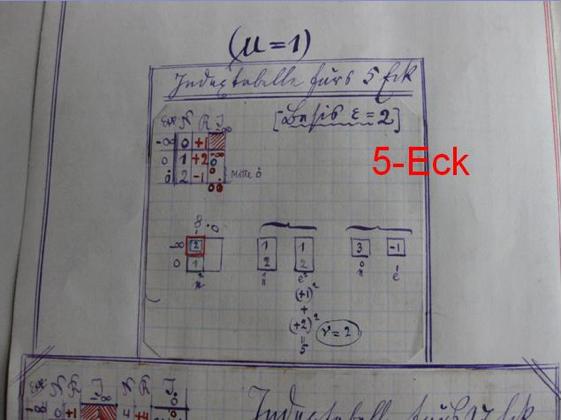
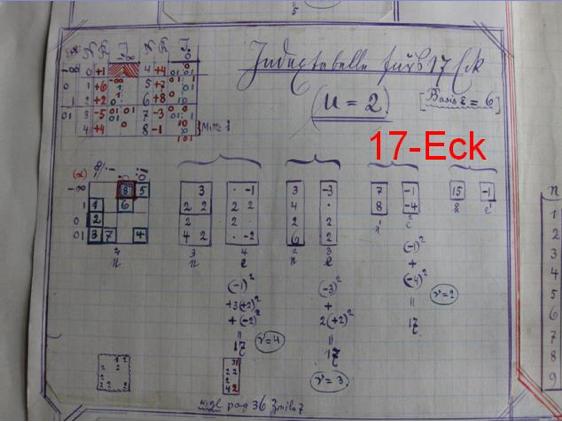
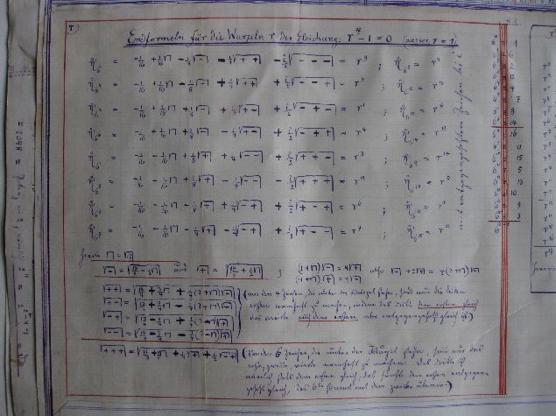
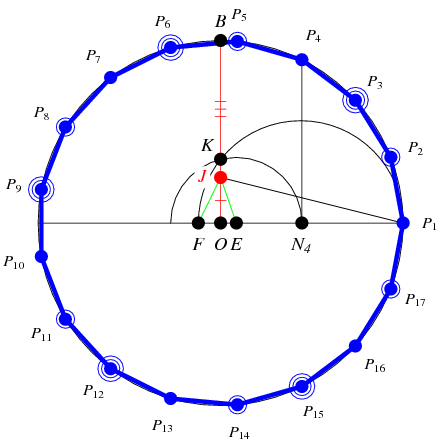
Computing the 65537-gon

While studying and teaching mathematics in Prussia and Germany, Johann Gustav Hermes (1846–1912) spent 10 years on a 200-page manuscript focusing on the construction of the 65537-gon. After the Second World War, Hermes's manuscripts were moved to the Mathematical Institute in Göttingen, where they can now be viewed in the so-called "suitcase of Göttingen."

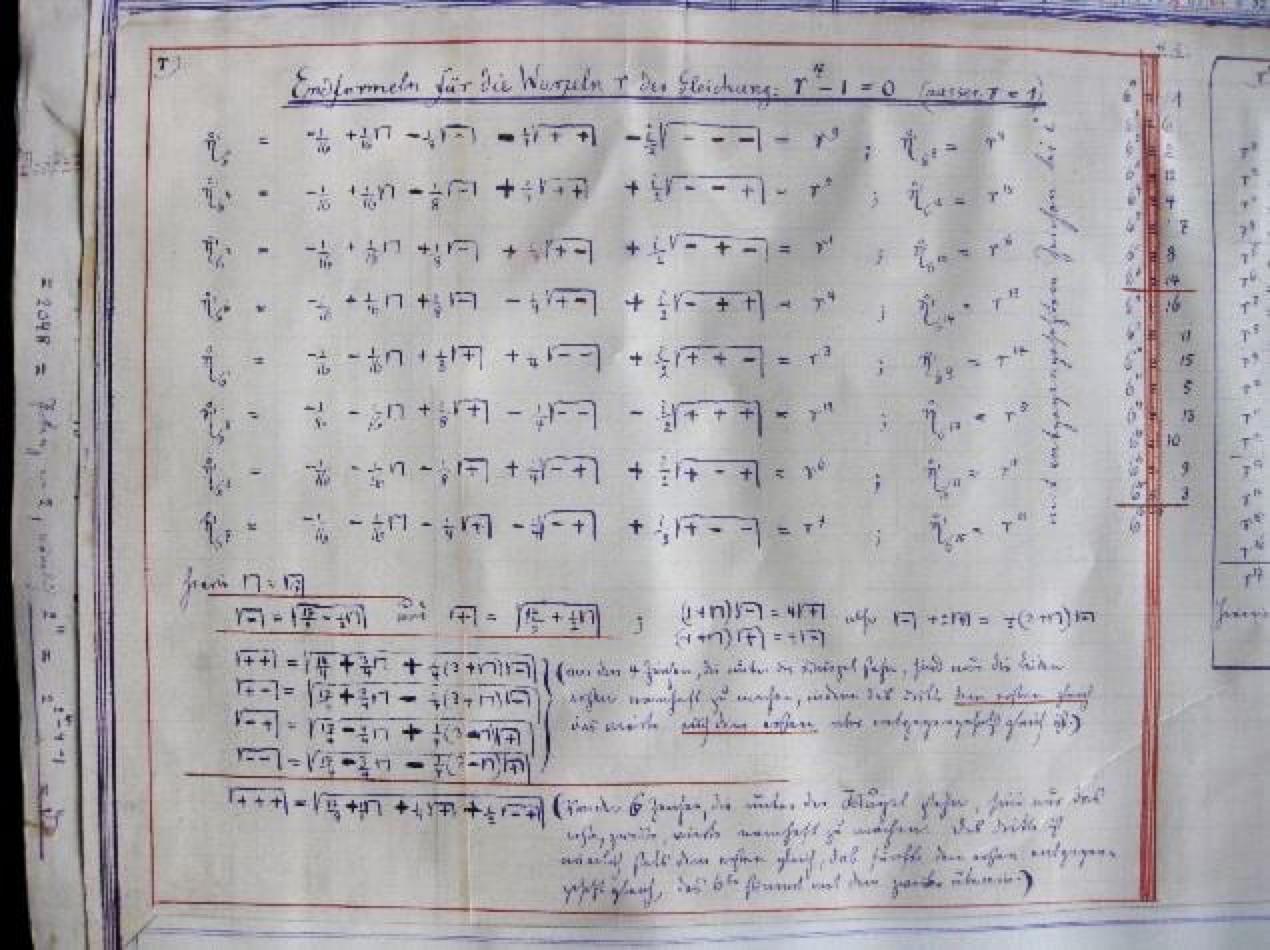
The 65537 sides in Hermes's computation are of interest because 65537 is the largest known Fermat prime. As such, it corresponds to the largest known "basic" (i.e. not having a number of sides which is a multiple of side counts of smaller constructible polygons) regular polygon that is constructible using classical Greek method involving compass and straightedge. However, despite the Herculean effort in computation and perseverance on the part of Hermes, the assessment of geometer H. S. M. Coxeter that "Hermes wasted ten years of his life on the 65537-gon" reflects the fact that not only do these calculations contain no new mathematics but—especially following the advent of symbolic computer algebra—they can be fully automated.

Artifact format

Suitcase containing 221 large-format pages

Artifact origin

Kaliningrad, Russia

Current artifact location

Georg-August-Universität Göttingen

Timeline

Interactive Content

Computational Explanation

The ancient Greek methods of geometric construction permitted the use of only two instruments: a straightedge and a compass. A straightedge is an idealized mathematical object having a rigorously straight edge that can be used to draw a line segment and upon which markings are not permitted. (As a result, the term "straightedge" is preferable to the sometimes-used "ruler" since the markings present on rulers are not permitted by the classical Greek rules.) A compass, on the other hand, is a tool consisting of two pivoting arms joined at one end that can be used to draw circles by placing one free arm at the center and rotating the other free arm through a full turn while keeping the distance between the arms fixed. In geometric constructions, the classical Greek rules stipulate that the compass cannot be used to mark distances, so it must "collapse" whenever one of its arms is removed from the page.

A number that can be represented by a finite number of additions, subtractions, multiplications, divisions and finite square root extractions of integers is called a "constructible number." Such numbers correspond to line segments that can be constructed using only straightedge and compass. All rational numbers are constructible, and all constructible numbers are algebraic numbers.

Compass and straightedge constructions dating back to Euclid were capable of constructing regular n-gons when

was of the form:

n

… k was a non-negative integer and

a,b0,1

. For n up to 100, the Greeks could therefore construct regular polygons with the following numbers of sides:

In[]:=

greek=Select[Range[3,100],DeleteCases[FactorInteger[#],{2,_}|{3|5,1}]==={}&]

Out[]=

{3,4,5,6,8,10,12,15,16,20,24,30,32,40,48,60,64,80,96}

These polygons are illustrated below, where, at the scale used, the polygons become visually indistinguishable from circles starting around

n30

sides:

In[]:=

GraphicsGrid[Partition[Graphics[{FaceForm[],EdgeForm[Black],RegularPolygon[#]}]&/@greek,UpTo[5]],ImageSizeLarge]

Out[]=

In 1796—more than two millennia after the original Greek investigators—a 19-year old Gauss extended the list of constructible polygons by proving the groundbreaking result that a sufficient (and later proved also necessary) condition for a regular polygon on n sides to be constructible is that n be of the form:

n

⋯

where

are distinct Fermat primes and k is again a non-negative integer. Here, a Fermat prime is a number of the form:



which is a prime number.

Fermat conjectured in 1650 that every Fermat number is prime and Eisenstein in 1844 proposed as a problem the proof that there are an infinite number of Fermat primes. At present, however, the only known Fermat primes correspond to

n0

, 1, 2, 3 and 4:

In[]:=

FermatPrimeIndices=Select[Range[0,15],PrimeQ[2^2^#+1]&]

Out[]=

{0,1,2,3,4}

… and are given by:

In[]:=

FermatPrimes=Table[2^2^p+1,{p,FermatPrimeIndices}]

Out[]=

{3,5,17,257,65537}

Gauss's proof for the 17-gon allows regular n-gon construction for the following values of n up to 100:

In[]:=

gauss=Select[Range[3,100],DeleteCases[FactorInteger[#],{2,_}|{3|5|17|257|65537,1}]==={}&]

Out[]=

{3,4,5,6,8,10,12,15,16,17,20,24,30,32,34,40,48,51,60,64,68,80,85,96}

As a result, Gauss's criterion allows a number of n-gon constructions unknown to the ancients, the smallest of which have the following values for n:

In[]:=

Complement[gauss,greek]

Out[]=

{17,34,51,68,85}

Interestingly, an equivalent statement to Gauss's criterion:

In[]:=

c1=Select[Range[3,10^6],DeleteCases[FactorInteger[#],{2,_}|{3|5|17|257|65537,1}]==={}&];//Timing

Out[]=

{4.20246,Null}

… states that n is constructible if and only if the Euler totient function of n is a power of 2 (Krížek et al. 2001, p. 34):

In[]:=

c2=Select[Range[3,10^6],MatchQ[FactorInteger[EulerPhi[#1]],{{2,_}}]&];//Timing

Out[]=

{5.95074,Null}

Checking reveals the lists indeed agree up to at least one million:

In[]:=

c1===c2

Out[]=

True

One method of constructing the heptadecagon (i.e. 17-gon) can be illustrated as follows (e.g. Coxeter 1969, pp. 26–28):

While the Wolfram Language can expand trigonometric functions having arguments that are rational multiples of π using FunctionExpand:

In[]:=

FunctionExpand[Cos[2π/17]]

Out[]=

15+

2(17-

)

234+6

2(17-

)

34(17-

)

2(17+

)



In[]:=

FunctionExpand[Sin[2π/17]]

Out[]=

215+

2(17-

)

234+6

2(17-

)

34(17-

)

-8

2(17+

)



… or ToRadicals:

In[]:=

ToRadicals[Cos[2π/17]]==FunctionExpand[Cos[2π/17]]

Out[]=

True

In[]:=

ToRadicals[Sin[2π/17]]==FunctionExpand[Sin[2π/17]]

Out[]=

True

… these expansions do not necessarily correspond to Gauss expansions. Happily, a Wolfram Function Repository function contributed by Michael Trott can compute such expansions, for example:

In[]:=

[◼]	Cos2PiOverFermatPrime

[17,Cos]

Out[]=

In[]:=

[◼]	Cos2PiOverFermatPrime

[17,Sin]

Out[]=

Symbolic computation can be used to confirm equivalence with the trigonometric functions:

In[]:=

FullSimplify

[◼]	Cos2PiOverFermatPrime

[17,Cos]-Cos[2π/17]

Out[]=

In[]:=

FullSimplify

[◼]	Cos2PiOverFermatPrime

[17,Sin]-Sin[2π/17]

Out[]=

The trigonometric expressions can also be reduced to roots of algebraic equations:

In[]:=

RootReduce/@{Cos[2π/17],Sin[2π/17]}

Out[]=



0.932

…

0.361

…



… in this case of orders 8 and 16, respectively.

Extending Gauss expansion to larger Fermat primes gives increasingly complicated expressions. For example, for

n257

, an elided form of the full expression is given by:

In[]:=

[◼]	Cos2PiOverFermatPrime

[257,Cos]//Short[#,4]&

Out[]//Short=

257

16+

257

16+

257

16+

257

+11+2

257

16+

257

(-1-1)+1+

(1)+

1

257

16+

257

(1)+1+

(1)+

1

(1)+11+

1

… but the full expression extends over many pages.

In the case of the 65537-gon considered by Hermes, the expressions are even more complicated. However, they can be computed by calling Cos2PiOverFermatPrime using the "Rules" argument to obtain a list of replacement rules that can be combined iteratively to obtain the full expression. For example, for the 17-gon:

In[]:=

Cos2PiOver17Rules=

[◼]	Cos2PiOverFermatPrime

[17,"Rules"]

Out[]=



C[1,2],C[1,16]-1,C[3,8]

C[1,16]-

C[1,16]

,C[1,8]

C[1,16]+

C[1,16]

,C[10,4]

C[3,8]-

C[3,8]

,C[9,4]

C[1,8]-

C[1,8]

,C[3,4]

C[3,8]+

C[3,8]

,C[1,4]

C[1,8]+

C[1,8]

,C[15,2]

C[9,4]+

1+C[1,8]+C[3,4]+

C[9,4]

,C[13,2]

C[1,4]-

C[1,4]

-C[3,4]

,C[11,2]

C[10,4]+

-C[1,4]+

C[10,4]

,C[10,2]

C[10,4]-

-C[1,4]+

C[10,4]

,C[9,2]

C[9,4]-

1+C[1,8]+C[3,4]+

C[9,4]

,C[5,2]

C[3,4]-

C[1,4]-C[1,8]+

C[3,4]

,C[3,2]

C[3,4]+

C[1,4]-C[1,8]+

C[3,4]

,C[1,2]

C[1,4]+

C[1,4]

-C[3,4]



Recursively applying the rules with the help of the Wolfram Language function ReplaceRepeated gives:

In[]:=

Cos2PiOver17=Apply[ReplaceRepeated,Cos2PiOver17Rules]

Out[]=

… which is the same expression that would have been obtained by directly calling the function with argument Cos:

In[]:=

[◼]	Cos2PiOverFermatPrime

[17,Cos]

Out[]=

Now compute the replacement rules for the 65537-gon:

In[]:=

{time,Cos2PiOver65537Rules}=

[◼]	Cos2PiOverFermatPrime

[65537,"Rules"]//Timing;

This takes a bit longer, but still requires less than a quarter of an hour:

In[]:=

UnitConvert[Quantity[time,"Seconds"],"Minutes"]

Out[]=

12.3261

min

Numericizing the result using 200 digits of fixed precision:

In[]:=

Clear[c];SetAttributes[c,NHoldAll];num65537=Set@@@N[Cos2PiOver65537Rules[[2]]/.Cc,200];Cos2PiOver65537=num65537[[-1]]/2;

... gives:

In[]:=

Cos2PiOver65537

Out[]=

0.9999999954042475651948688244124392033237035566190698219615158713718364117933218107442834915097270826816226674472317553123866034865209595511870325419891382667702120134005174484344868

… which has 181 digits of precision:

In[]:=

Cos2PiOver65537//Precision

Out[]=

181.76

As expected, the value is very close to 1 since the cosine of a small argument ≈ 1.

Comparing to the value computed directly from the cosine shows agreement to within the expected precision:

In[]:=

Cos

2π

65537

-hermesCos

Out[]=

0.×

-182

Since the above construction process was purely programmatic and fully implemented using symbolic computer algebra, the assessment of geometer H. S. M. Coxeter that "Hermes wasted ten years of his life on the 65537-gon" is borne out by noting that the crucial part of Hermes's monumental 10-year computation can now be replicated using less than a quarter-hour of automated computation.

Other Resources

Additional Reading

Bold, B. Famous Problems of Geometry and How to Solve Them. New York: Dover, p. 70, 1982.
Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: Wiley, 1969.
Dixon, R. Mathographics. New York: Dover, p. 53, 1991.
Hermes, J. "Über die Teilung des Kreises in 65537 gleiche Teile." Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse, Vol. 3. Göttingen, pp. 170–186, 1894.
Krížek, M.; Luca, F. and Somer, L. 17 Lectures on Fermat Numbers: From Number Theory to Geometry. New York: Springer-Verlag, 2001.
Trott, M. "cos(2π/257) à la Gauss." § 1.10.2 in The Mathematica GuideBook for Symbolics. New York: Springer-Verlag, pp. 312–321, 2006.
Young, J. (Ed.). "Leonard Eugene Dickson Constructions with Ruler and Compasses; Regular Polygons." Ch. 8 in Monographs on Topics of Modern Mathematics Relevant to the Elementary Field. New York: Dover, pp. 352–386, 1955.