History of Mathematics Project | Cataldi's Divisor Table

History of
Mathematics

Project

1603

Cataldi's Divisor Table

Oldest divisor table, giving divisors for numbers up to 750

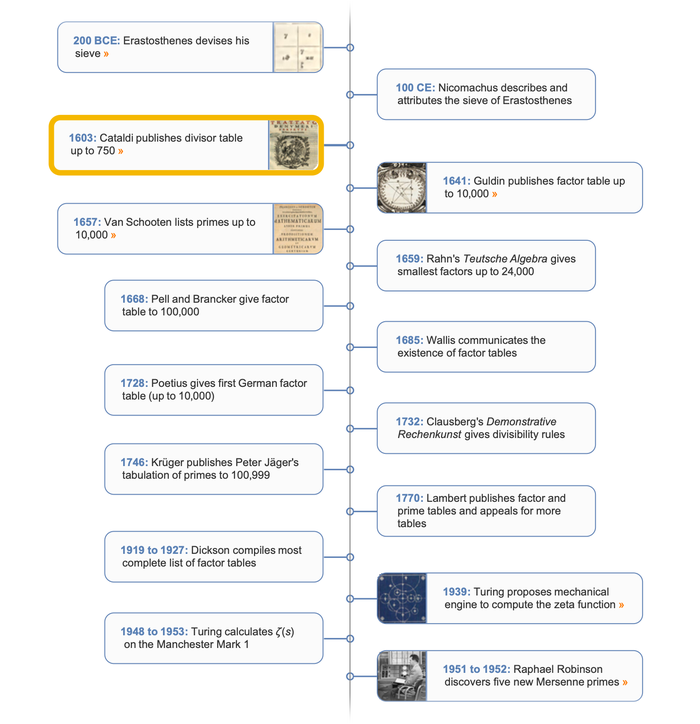
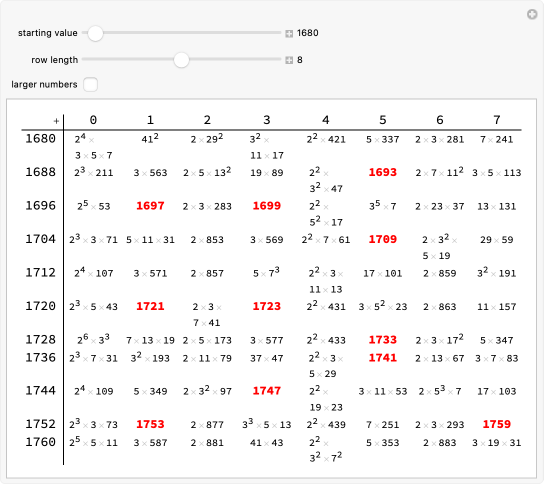
Cataldi wrote the first divisor table in 1588, publishing a table of divisors up to 750 (extended to 800 in a supplement) in 1603.

The oldest divisor table is due to Cataldi, who gave a list of the divisors of all numbers to 750 (extended to 800) in connection with his study of perfect numbers. The work was composed in 1588 and published in Bologna in 1603. Cataldi proved with the help of his table that Mersenne numbers 2^17 - 1 and 2^19 - 1 were prime and asserted that exponents 23, 29, 31, 37 also generated perfect numbers. The assertion was later proven false (with the exception of 31) by Fermat and Euler.

Artifact dimensions

5.8 in. × 7.8 in. (52 pages)

Artifact origin

Bologna, Italy

Timeline

Interactive Content

Computational Explanation

Cataldi's table consisted of lists of nontrivial proper divisors (i.e. divisors of a number

other than 1 and

itself). Proper divisors are easy to compute in the Wolfram Language:

In[]:=

NontrivialProperDivisors[1]:={}NontrivialProperDivisors[n_Integer]:=Divisors[n][[2;;-2]]

For example, the divisors of 30 are:

In[]:=

Divisors[30]

Out[]=

{1,2,3,5,6,10,15,30}

… while the nontrivial proper divisors are given by:

In[]:=

NontrivialProperDivisors[30]

Out[]=

{2,3,5,6,10,15}

As can be seen, the list of six factors above is in agreement with Cataldi's list:

Performing the process on the numbers 2 through 30 gives the first page of Cataldi's table:

TextGrid[Transpose[Partition[Table[If[PrimeQ[n],n,Row[{n,Row[Riffle[NontrivialProperDivisors[n],"."]]},Spacer[3]]],{n,30}],10]/.{Row[{1,_},___],l__}{l,""}],Spacings2]

Out[]=

2	11	21 3.7
3	12 2.3.4.6	22 2.11
4 2	13	23
5	14 2.7	24 2.3.4.6.8.12
6 2.3	15 3.5	25 5
7	16 2.4.8	26 2.13
8 2.4	17	27 3.9
9 3	18 2.3.6.9	28 2.4.7.14
10 2.5	19	29
	20 2.4.5.10	30 2.3.5.6.10.15

Such computations are simple for modern digital computers, which are capable of factoring all positive integers up to 10,000 in a fraction of a second:

In[]:=

divisors=Divisors[Range[10^4]];//Timing

Out[]=

{0.026676,Null}

The count of the number of divisors of a number

(including 1 and

) is denoted

(n)

and can be computed more directly using the Wolfram Language function DivisorSigma:

In[]:=

Length/@divisors===DivisorSigma[0,Range[10^4]]

Out[]=

True

Plotting the values up to various limits shows a number of interesting patterns and band-like structures:

In[]:=

Table[ListPlot[DivisorSigma[0,Range[10^n]]],{n,4}]

Out[]=





Now, instead of the number of divisors

(n)

, consider the sum-of-divisors function denoted

(n)

. Again, plotting this for ranges of numbers shows interesting patterns:

In[]:=

Table[ListPlot[DivisorSigma[1,Range[10^n]]],{n,4}]

Out[]=





Numbers

that are equal to the sum of their proper divisors (including 1 but excluding

itself) are said to be perfect numbers. For example, 6 = 1 + 2 + 3, so 6 is a perfect number. Perfect numbers were studied by the ancient Greeks and were the motivation for Cataldi to compute his divisor table. For example, the first several perfect numbers are:

In[]:=

Select[Range[10^4],DivisorSigma[1,#]-##&]

Out[]=

{6,28,496,8128}

Perfect numbers are intimately connected with a class of numbers known as Mersenne primes, which are prime numbers of the form



-1

. As stated in Proposition IX.36 of Euclid's Elements, if

is prime, then

(

+1)



p-1

(

-1)

is a perfect number.

Cataldi proved with the help of his table that Mersenne numbers

-1

and

-1

were prime and asserted that exponents 23, 29, 31, 37 also generated perfect numbers. The assertion was later proven false (with the exception of 31) by Fermat and Euler, as can be easily verified computationally:

In[]:=

Select[Range[40],PrimeQ[2^#-1]&]

Out[]=

{2,3,5,7,13,17,19,31}

Other Resources

History of Mathematics
Guldin's Factor Table

History of Mathematics
Van Schooten's Prime Table

Wolfram Demonstration
Prime Factorization Table

Additional Reading

Bullynck, M. "Factor Tables 1657–1817, with Notes on the Birth of Number Theory." Revue d'Histoire des Mathematiques, Vol. 16, No. 2, pp. 133–216, 2010.
Cataldi, A. Trattato de’ numeri perfetti. Bologna, Italy: presso gli heredi di Giouanni Rossi, 1603.